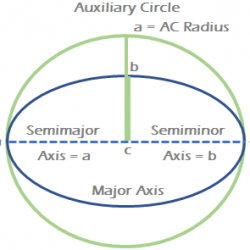
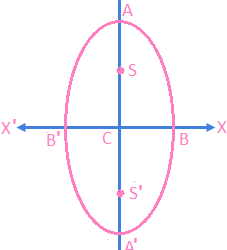
Auxiliary circle of an ellipse which is a circle described on the major axis of an ellipse as its diameter. Let the ellipse be … (1)Then the equation of its auxiliary circle is x² + y² = a² … (2) Take a point P(x₁, y₁) on (1). Through P, draw a line perpendicular to major axis intersecting major axis in N and auxiliary Read more about Auxiliary Circle of an Ellipse […]
A rectangular hyperbola is also known as an equilateral hyperbola. The asymptotes of rectangular hyperbola are y = ± x. If the axes of the hyperbola are rotated by an angle of -π/4 about the same origin, then the equation of their rectangular hyperbola x² – y² = a² is reduced to or xy = c². 1) A hyperbola whose asymptotes include a right angle Read more about Rectangular Hyperbola[…]
Fundamental Terms Hyperbola Conjugate Hyperbola (a) Equation (b) Graph (c) Centre C (0, 0) C (0, 0) (d) Vertices (±a, 0) (0, ±b) (e) Length of transverse axis 2a 2b (f) Length of conjugate axis 2b 2a (g) Foci (±ae, 0) (0, ±be) (h) Equation of directrices (i) Eccentricity (j) Length of latus Read more about Hyperbola[…]
Hyperbola: A hyperbola (plural hyperbolas or hyperbolae) is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. The hyperbola is one of the three kinds of conic section, formed by the intersection of a plane and a double cone. Focus – The two fixed points which defines the hyperbola are called Read more about Terms related to Hyperbola[…]
Terms Related to an Ellipse: Fundamental Terms Ellipse (Horizontal ellipse) Conjugate Ellipse(Vertical ellipse) (a) Equation (b) Graph (c) Centre C (0, 0) C (0, 0) (d) Vertices (±a, 0) (0, ±b) (e) Length of major axis 2a 2b (f) Length of minor axis 2b 2a (g) Foci (±ae, 0) (0, ±be) (h) Equation of directrices Read more about Ellipse[…]
Definition: If the axes are rotated through an any angle in the same plane by keeping the origin constant, then the transformation is called Rotation of axes. Theorem: To find the co-ordinates of point (x, y) at a point are transformed to (X, Y). When the axes are rotated through an angle about the origin Read more about Rotation Axes[…]
Straight line is the locus of a moving point P (h, k), which moves in such a condition that P is always collinear with the given two fixed points.Ex: various forms of straight lines:General form: The most general equation of a straight line is ax + by + c = 0, where a, b and c are any real numbers Read more about Straight Lines[…]
Row Matrix: A matrix having a single row is called a row matrix. Example: Column Matrix: A matrix having a single column is called a column matrix. Example: . Square Matrix: An m x n matrix A is said to be a square matrix if m = n i.e. number of rows = number of columns. Read more about Classification of Matrices[…]
Case (1): Radical axis of the two circles is defined as the line from each point of which, tangents of equal length are drawn to the two circles.Where T = T₁ Case (2): In case of three circles radical point can be defined as the point where radical axis of three circles taken two at Read more about Radical Axis of the Two Circles[…]
The angle of intersection between two curves intersecting at a point is the angle between their tangents drawn at that point. The curves are said to be intersecting orthogonally, if the angle between their tangents are common point is a right angle. Consider two circles S₁ ≡ x² + y² + 2g₁x + 2f₁y + C₁ = 0 S₂ ≡ Read more about Two Circles Intersect Orthogonally[…]