A rectangular hyperbola is also known as an equilateral hyperbola. The asymptotes of rectangular hyperbola are y = ± x. If the axes of the hyperbola are rotated by an angle of -π/4 about the same origin, then the equation of their rectangular hyperbola x² – y² = a² is reduced to \(xy\text{ }=\frac{{{a}^{2}}}{2}\) or xy = c².
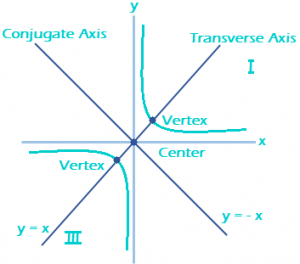
1) A hyperbola whose asymptotes include a right angle is called a rectangular Hyperbola. The general form of the equation of hyperbola is x² – y² = a² – b².
The asymptotes of a hyperbola is \(y\,=\,\frac{\pm bx}{a~}\).
If these are at right angles than m₁m₂ = -1.
⇒ \(\frac{b}{a}\left( -\frac{b}{a} \right)=-1\)
b² = a²
Hence the equation of rectangular hyperbola is \(\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{{{y}^{2}}}{{{a}^{2}}}=1\)
x² – y² = a².
(2) If the length of transverse & conjugate axes of any hyperbola are equal, it is called as rectangular hyperbola.
IF a = b, then \(\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{{{y}^{2}}}{{{b}^{2}}}=1\) become is \(\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{{{y}^{2}}}{{{a}^{2}}}=1\)
x² – y² = a².
