Terms related to Hyperbola

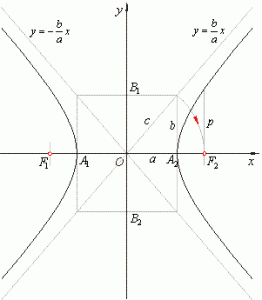
Hyperbola:

• A hyperbola (plural hyperbolas or hyperbolae) is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set.
• The hyperbola is one of the three kinds of conic section, formed by the intersection of a plane and a double cone.
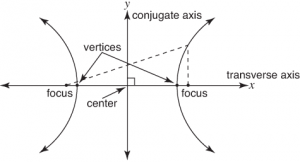
• Focus – The two fixed points which defines the hyperbola are called the focus together called Foci.
• Center – It is the midpoint of the line segment which joins the two foci. Or the intersection point of the transverse axis and the conjugate axis.
• Transverse Axis – It is a line passes through the two foci. It is also called the major axis of hyperbola.
• Conjugate Axis – It is the line perpendicular to transverse axis and passé through the center of the hyperbola.
• Vertex – The two points where the hyperbola intersects with the transverse axis are called the Vertextogether called Vertices.

Terms and Formulae

• Focus of Hyperbola
• Asymptotes of Hyperbola
• Eccentricity of Hyperbola
• Latus rectum of Hyperbola
• Semi Latus Rectum
• Rectangle in Hyperbola

1. Focus of Hyperbola: Focus is a point from which the distance is measured to form conic. The Hyperbola has two foci.to calculate the focus we can use the formula
   \(c=\sqrt{{{a}^{2}}+{{b}^{2}}}\).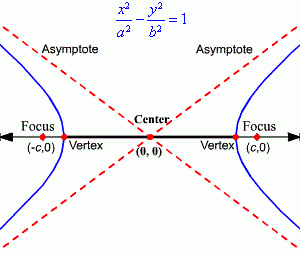

2. Asymptotes of Hyperbola: These are the two intersecting straight lines in a hyperbola which intersects at the center.If a hyperbola retreats from the center, its branches approach these asymptotes. The equation of asymptotes are:
   y = (b/a) x
   y = − (b/a) x.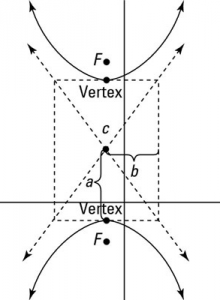

3. Eccentricity of Hyperbola: The eccentricity of Hyperbola is the ratio of the distance between the focus and a point on the plane to the vertex and that point only.
   As the Hyperbola is a locus of all the points which are equidistant from the focus and the directrix, its ration will always be 1 that is, e = c/a.
   where, \(c=\sqrt{{{a}^{2}}+{{b}^{2}}}\)
   In hyperbola e > 1 that is, eccentricity is always greater than 1.

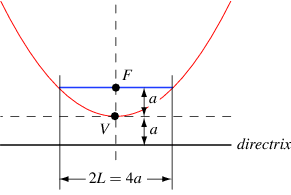
4. Latus rectum of Hyperbola: It is the line perpendicular to transverse axis and passes through any of the foci of the hyperbola. It is parallel to the conjugate axis.
   In Hyperbola, latus rectum is 2b²/a.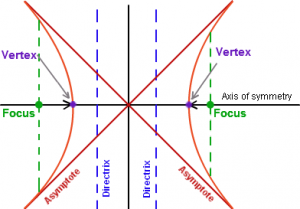

5. Semi Latus Rectum: It is the half of the latus rectum as shown in the above picture as p. so p = b²/a.
6. Rectangle in Hyperbola: It is the rectangle made by the a and b which helps in drawing the hyperbola. A is the distance between the center and the vertex, b is the half length of the conjugate axis and c is the distance between center and the focus. The diagonal of this rectangle intersects at the center and these diagonals are the asymptotes of hyperbola.