Definition: If the axes are rotated through an any angle in the same plane by keeping the origin constant, then the transformation is called Rotation of axes.
Theorem: To find the co-ordinates of point (x, y) at a point are transformed to (X, Y). When the axes are rotated through an angle about the origin then x = X cosθ – Y sinθ, y = X sinθ + Y cosθ.
Proof: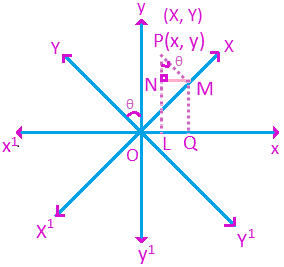
Let x¹ox, yoy¹ be the original axes
LetX¹ox, Yoy¹ be the New axes
Then ∠xoX = θ, ∠Yoy = θ
Let P be the given point whose co-ordinate are (x, y) with reference to the original axes and (X, Y) with reference to the new axes.
Let L, M be the projections of P on \(\overleftrightarrow{{{x}^{1}}ox}\) and \(\overleftrightarrow{{{x}^{1}}ox}\)respectively.
Let N, Q be the projections of M on \(\overleftrightarrow{{{x}^{1}}ox}\) and \(\overleftrightarrow{PL}\) respectively
Now ∠QPM = 0
From OMN \(\cos \theta =\frac{ON}{OM},\,\sin \theta =\frac{MN}{ON}\Rightarrow ON\)
= OM cosθ, MV = OM sinθ
From \(\Delta PQM\,\cos \theta =\frac{PQ}{PM}\)
\(\operatorname{Sin}\theta =\frac{QM}{PM}\)
⇒ PQ = PM cosθ
⇒ QM = PM sinθ
x = OL = ON – LN = ON – QM
= OM cosθ – PM sinθ
= X cosθ – Y sinθ
y = PL = PQ + QL = PQ + MN = PM cosθ + OM sinθ.
⇒ Y cosθ + X sinθ … 1
The equation x = X cosθ – Y sinθ … 2
Sol equation 1 and 2 we wil get
X = x cosθ + y sinθ
Y = -x sinθ + y cosθ
| X |
Y |
|
|
X |
cosθ |
-sinθ |
|
Y |
sinθ |
Cosθ |
Ex: When the axes are rotated through an angle 30 find the new co-ordinates of the following point
i) (0, 5)
Sol: Given that θ = 30⁰
Old co-ordinates are (0, 5)
i,e , x = 0 , y= 5
X = x cosθ + Y sinθ
Y = – x sinθ + y cosθ
Y = – 0 sin30⁰ + 5 cos 30⁰ \(Y=-0\sin {{30}^{0}}+5\cos {{30}^{0}}=\frac{5\sqrt{3}}{2}\)
New co-ordinates are \(\left( \frac{5}{2},\frac{5\sqrt{3}}{2} \right)\)