Case (1): Radical axis of the two circles is defined as the line from each point of which, tangents of equal length are drawn to the two circles.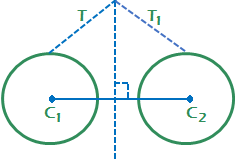 Where T = T₁
Where T = T₁
Case (2): In case of three circles radical point can be defined as the point where radical axis of three circles taken two at a time intersect. It is the point from which tangent of equal length can be drawn to all the three circles.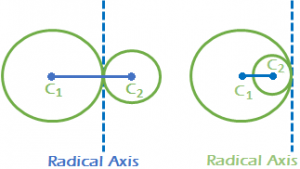 If S ≡ x² + y² + 2gx + 2fy + c
If S ≡ x² + y² + 2gx + 2fy + c
S’ ≡ x² + y² + 2g’x + 2f’y+ c’
Then equation of radical axis of two circles.
S = 0 and S’ = 0 is given by S = S’
i.e. x² + y² + 2gx + 2fy + c = x² + y² + 2g’x + 2f’y + c’
2(g – g’)x + 2(f – f’)y + (c – c’) = 0.
Case (3):
(i) If the circles touch each other then the above equation gives the common tangent at the point where the circles touch each other. It is also the Radical axis of the two circles. 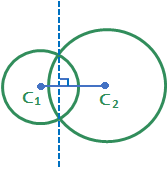 (ii) If the two circles intersect then above equation gives the equation of the common chord. Here also the common chord is also the Radical axis of the two circles. Two circles with centers C₁ (x₁, y₁) and C₂ (x₂, y₂) and radii r₁, r₂ respectively, touch each other.
(ii) If the two circles intersect then above equation gives the equation of the common chord. Here also the common chord is also the Radical axis of the two circles. Two circles with centers C₁ (x₁, y₁) and C₂ (x₂, y₂) and radii r₁, r₂ respectively, touch each other.
(iii) Internally: If |C₁C₂| = |r₂ – r₁| and the point of contact is \(\frac{\left( {{r}_{1}}~{{x}_{2~}}-\text{ }{{r}_{2}}~{{x}_{1}} \right)}{{{r}_{1}}+{{r}_{2}}},\frac{\left( {{r}_{1}}{{y}_{2~}}-\text{ }{{r}_{2}}{{y}_{1}} \right)}{{{r}_{1}}+{{r}_{2}}}\).
(iv) Externally: If |C₁C₂| = |r₂ – r₁| and the point of contact is \(\frac{\left( {{r}_{1}}~{{x}_{2~}}\text{+ }{{r}_{2}}~{{x}_{1}} \right)}{{{r}_{1}}+{{r}_{2}}},\frac{\left( {{r}_{1}}{{y}_{2~}}\text{+ }{{r}_{2}}{{y}_{1}} \right)}{{{r}_{1}}+{{r}_{2}}}\).
