The angle of intersection between two curves intersecting at a point is the angle between their tangents drawn at that point. The curves are said to be intersecting orthogonally, if the angle between their tangents are common point is a right angle.
Consider two circles
S₁ ≡ x² + y² + 2g₁x + 2f₁y + C₁ = 0
S₂ ≡ x² + y² + 2g₂x + 2f₂y + C₂ = 0
They intersect at point P such that tangent PT₁ and PT₂ are at right angle.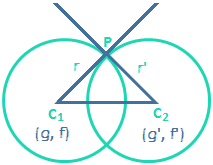
Since radius of a circle is perpendicular to the tangent. So C₁P and C₂P are also perpendicular.
⇒ (C₁C₂)² = (C₁P)² + (C₂P)²
⇒ (g₁ – g₂)² + (f₁ – f₂)² = r₁² + r₂²
⇒ g₁² + g₂² – 2g₁g₂ + f₁² + f₂² – 2f₁f₂ = g₁² + f₁² – C₁ + g₂² + f₂² – c²
⇒ 2g₁g₂ + 2f₁f₂ = C₁ + C₂
Ex: Find the equation of the circle which cuts orthogonally the circle x² + y² – 4x + 2y – 7 = 0 and having center at (2, 3).
Sol: Given that x² + y² – 4x + 2y – 7 = 0 … 1
Required circle is S ≡ x² + y² + 2gx + 2fy + C = 0
And center is (2, 3) = (-g, -f)
Equation 1 center is (2, -1) = (-g’, -f’)
S = 0 circle cuts the orthogonally S’ = 0
2(gg’ + ff’) = C + C’
2((-2) (-2) + (-3) (1)) = C + (-7)
8 – 6 = C – 7
C = 9
Required circle is x² + y² – 4x – 6y + 9 = 0.