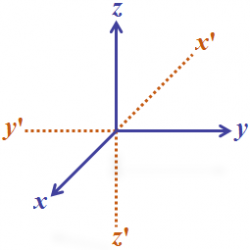
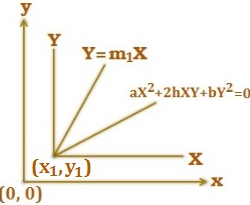
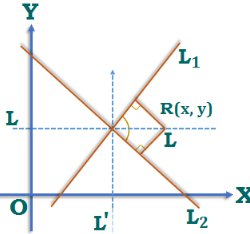
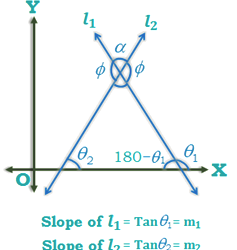
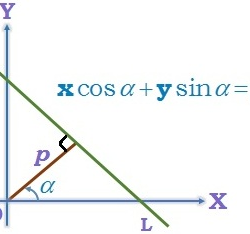
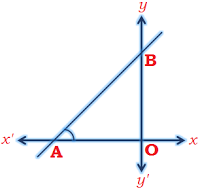
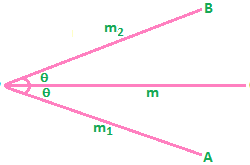
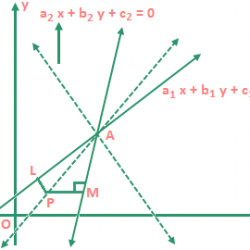
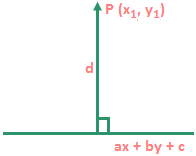
Co – ordinates of point in space
Let X’OX, Y’OY and Z’OZ be three mutually perpendicular lines intersecting at O such that two of them viz. Y’OY and Z’OZ lie in the plane of the paper and the third X’OX is perpendicular to the plane of the paper and is projecting out from the plane of the paper (see Fig shown below.). Read more about Co – ordinates of point in space[…]