Condition for the lines to be coincident: The lines are coincident if the angle between them is zero. Thus, lines are coincident.
⇒ θ = 0
⇒ tanθ = 0
⇒ \(\frac{2\sqrt{{{h}^{2}}-ab}}{a+b}=0\).
⇒ h2 – ab = 0
⇒ h2 = ab
Hence, the lines represented by ax2 + 2hxy + by2 = 0 are coincident if h2 = ab.
Condition for the lines to be perpendicular: The lines are perpendicular if the angle between them is π/2.
Thus, lines are perpendicular.
⇒ θ = π/2
⇒ cot θ = cot π/2
⇒ cot θ = 0
⇒ \(\frac{a+b}{2\sqrt{{{h}^{2}}-ab}}=0\).
⇒ a + b = 0
⇒ coeff of x² + coeff of y² = 0
Thus, the lines represented by ax² + 2hxy + by² = 0 are perpendicular if a + b = 0 i.e., coeff. of x2 + coeff. of y2 = 0
GENERAL EQUATION OF SECOND DEGREE: The necessary and sufficient condition for ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 to represent a pair of straight lines is that abc + 2fgh – af2 – bg2 – ch2 = 0 or, \(\left| \begin{matrix} a & h & g \\ h & b & f \\ g & f & c \\\end{matrix} \right|=0\).
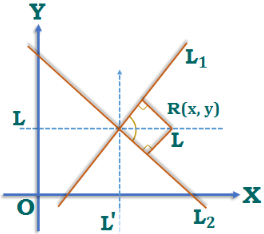
EQUATIONS OF THE BISECTORS: The equations of the bisectors of the angles between the lines (L₁, L₂) represented by ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 are given by \(\frac{{{\left( x-{{x}_{1}} \right)}^{2}}{{\left( y-{{y}_{1}} \right)}^{2}}}{a-b}=\frac{\left( x-{{x}_{1}} \right)\left( y-{{y}_{1}} \right)}{h}\), where (x1, y1) the point of intersection of the lines is represented by the given equation.