Normal or perpendicular form of a line: The equation of the straight line upon which the length of the perpendicular from the origin is P and this perpendicular makes an angle α with x – axis is x cosα + y sinα = P.
Example: A line forms a triangle of area 54√3 sq units with the coordinate axes. Find the equation of the line if the perpendicular drawn from the origin to the line makes an angle of 600 with the x – axis.
Solution: Let p be the length of the perpendicular drawn from the origin to the required line. The perpendicular makes an angle of 600 with the x-axis. So, the equation of the line is x cos600 + y sin 600 = p.
Or, x + √3y = 2p.
This cuts the coordinate axes at A (2p, 0) and B (0, 2p/√3).
It is given that
Area of ∆OAB = 54√3 Squints
⇒ ½ (OA) (OB) = 54√3
⇒ ½ x 2p x 2p/√3 = 54√3
⇒ p2 = 81
⇒ p = 9
Hence the equation of the line is x + √3y = 18.
Reduction of the general equation of a line to the normal form: The general equation of a line is Ax + By + C = 0 and its normal form be x cosα + y sinα = P.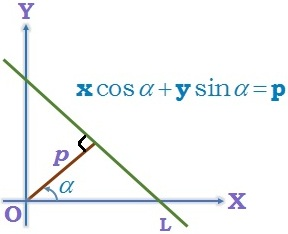
To reduce the general equation of a line to normal form, we first shift the constant term on the RHS and make it positive if it is not so and then divide both sides by \(\sqrt{{{\left( coeff\,of\,x \right)}^{2}}+{{\left( coeff\,of\,y \right)}^{2}}}\) i.e., \(\left( \frac{A}{\sqrt{{{A}^{2}}+{{B}^{2}}}} \right)x+\left( \frac{B}{\sqrt{{{A}^{2}}+{{B}^{2}}}} \right)y=\left( \frac{-C}{\sqrt{{{A}^{2}}+{{B}^{2}}}} \right)\).
Distance form of a line: The equation of the straight line passing through (x1, y1) and making an angle θ with the positive direction of x-axis is \(\frac{x-{{x}_{1}}}{\cos \theta }=\frac{y-{{y}_{1}}}{\sin \theta }=r\). Where r is the distance of a point (x, y) on the line from the point (x1, y1)
The coordinates of any point on the line at a distance from the given point (x1, y1) are (x1 ± r cosθ, y1 ± r sinθ). If the point is on the right side of (x1, y1), then r is positive and if the point is on the left side of(x1, y1), then r is negative.
Example: A straight line is drawn through the point P (2, 3) and is inclined at an angle of 300 with the x-axis. Find the coordinates of two points on it at a distance 4 from P on either side of P?
Solution: Here, (x1, y1) = (2, 3) and θ = 300. So, the equation of line is
\(\frac{x-2}{\cos {{30}^{0}}}=\frac{y-3}{\sin {{30}^{0}}}\).
Or, \(\frac{x-2}{\left( \frac{\sqrt{3}}{2} \right)}=\frac{y-3}{\left( \frac{1}{2} \right)}\)
Or, x – 2 = √3(y – 3)
Or, x – √3y = 2 – 3√3
Points on the line at a distance 4 from P (2, 3) are given by (x1 ± r cosθ, y1 ± r sinθ)
Or, (2 ± 4 cos300, 2 ± 4 sin300)
Or, (2 ± 2√3, 2 ± 2)
Or, (2 + 2√3, 4) and (2 – 2√3, 0)