A straight line is a curve such that every point on the line segment joining any two points on it lies on it.
Slope (Gradient) of a line: The trignometrical tangent of the angle that a line makes with the positive direction of the x – axis in anticlockwise sense is called the slope or gradient of the line.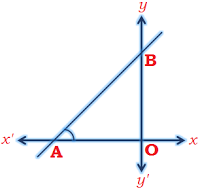
The slope of a line is generally denoted by m.
m = tanθ
The angle of inclination of a line with the positive direction of x – axis in anticlockwise sense always lies between 00 and1800.
The slope of a line joining (x₁, y₁) and (x₂, y₂) is given by \(m=\frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}=\frac{Difference\,of\,ordinates}{Difference\,of\,abscissae}\).
Various forms of equation of straight lines:
Slope intercept form of a line: The equation of a line with slope m and making an intercept c on y – axis is y = mx + c.
If the line passes through the origin, then 0 = m0 + c ⇒ c = 0
Therefore, the equation of a line passing through the origin is y = mx
If the line is parallel to x – axis, then m = 0 therefore the equation of a line parallel to x – axis is y = c.
Reduction of general form to slope intercept form: The general form of equation of a line is Ax + By + C = 0.
⇒ By = – Ax – C
⇒ \(y=\left( -\frac{A}{B} \right)x+\left( \frac{-C}{B} \right)\).
This is of the form y = mx + c, where \(m=\frac{-A}{B}\) and \(c=\frac{-C}{B}\).
Point – Slope form of a line: The equation of a line which passes through the point (x1, y1) and has the slope ‘m’ is y – y1 = m (x – x1)
Example: Find the equation of a line passing through (2, -3) and inclined at an angle 1350 with the positive direction of x – axis.
Solution: Here, m = slope of the line = tan 1350 = tan (900 + 450).
= – cot 450
= -1
And x1 = 2, y1 = -3.
So, the equation of the line is y – y1 = m (x – x1)
Or, y – (-3) = -1 (x – 2)
Or, y + 3 = – x + 2 or x + y + 1 = 0
Two point form of a line: The equation of a line passing through two points (x1, y1) and (x2, y2) is \(y-{{y}_{1}}=\left( \frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} \right)\left( x-{{x}_{1}} \right)\).
The equation of a line passing through two points (x1, y1) and (x2, y2) can also be written in the determinant form \(\left| \begin{matrix}x & y & 1 \\{{x}_{1}} & {{y}_{1}} & 1 \\{{x}_{2}} & {{y}_{2}} & 1 \\\end{matrix} \right|=0\).
Intercept form of a line: The equation of a line which cuts off intercepts a and b respectively from the x and y – axis is \(\frac{x}{a}+\frac{y}{b}=1\).
Reduction of general equation of a line to intercept form: The general equation of a line is Ax + B y + C = 0
⇒ Ax + By = – C
⇒ \(\frac{Ax}{-C}+\frac{By}{-C}=1\)
⇒ \(\frac{x}{\left( \frac{-C}{A} \right)}+\frac{y}{\left( \frac{-C}{B} \right)}=1\)
This is of the form \(\frac{x}{a}+\frac{y}{b}=1\)
Intercept on x-axis = \(\frac{-C}{A}\)
Intercept on y-axis = \(\frac{-C}{B}\)
The intercept made by a line on x-axis can also be obtained by putting y = 0 in its equation. Similarly, y-intercept is the value of y obtained from the line when x is replaced by zero.