Let X’OX, Y’OY and Z’OZ be three mutually perpendicular lines intersecting at O such that two of them viz. Y’OY and Z’OZ lie in the plane of the paper and the third X’OX is perpendicular to the plane of the paper and is projecting out from the plane of the paper (see Fig shown below.). Let O be the origin and the lines X’OX, Y’OY and Z’OZ be x – axis, y – axis and z – axis respectively.
These three lines are also called the rectangular axes of coordinates.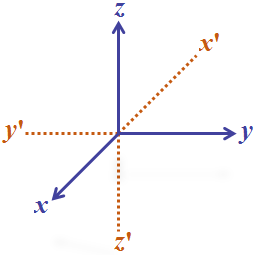
The planes containing the lines X’OX, Y’OY and Z’OZ in pairs, determine three mutually perpendicular planes XOY, YOX AND ZOZ or simply XY, YZ and ZX which are called rectangular coordinate planes.
Signs of Co-Ordinates of a Point:
| Octant | OXYZ | OX’YZ | OXY’Z | OX’Y’Z | OXYZ’ | OX’YZ’ | OXY’Z’ | OX’Y’Z’ | |
| Coordinates | X | + | – | + | – | + | – | + | – |
| Y | + | + | – | – | + | + | – | – | |
| Z | + | + | + | + | – | – | – | – |
Distance Formula: The distance between the points P (x₁, y₁, z₁) and Q (x₂, y₂, z₂) is given by \(PQ=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}}\).
If 0 is the origin and P(x, y, z) is a point in space, then \(OP=\sqrt{{{\left( x-0 \right)}^{2}}+{{\left( y-0 \right)}^{2}}+{{\left( z-0 \right)}^{2}}}=\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}\).
Example 1: Find the distance between the points P (-2, 4, 1) and Q (1, 2, – 5).
Solution: We have,
\(PQ=\sqrt{{{\left( 1-\left( -2 \right) \right)}^{2}}+{{\left( 2-4 \right)}^{2}}+{{\left( -5-1 \right)}^{2}}}\).
= \(\sqrt{9+4+36}\) = 7 units
Section Formulae:
Let P (x₁, y₁, z₁) and Q (x₂, y₂, z₂) be two points in space and let R be a point on the line segment joining P and Q such that it divides the join of P and Q internally in the ratio m₁ : m₂. Then the coordinates of R are \(\left( \frac{{{m}_{1}}{{x}_{2}}+{{m}_{2}}{{x}_{1}}}{{{m}_{1}}+{{m}_{2}}},\,\frac{{{m}_{1}}{{y}_{2}}+{{m}_{2}}{{y}_{1}}}{{{m}_{1}}+{{m}_{2}}},\,\frac{{{m}_{1}}{{z}_{2}}+{{m}_{2}}{{z}_{1}}}{{{m}_{1}}+{{m}_{2}}} \right)\)
If R is the mid-point of the segment joining P (x1, y1, z1) and Q (x2, y2, z2) then m₁ = m₂ = 1 and so the coordinates of R are given by \(\left( \frac{{{x}_{1}}+{{x}_{2}}}{2},\,\frac{{{y}_{1}}+{{y}_{2}}}{2},\,\frac{{{z}_{1}}+{{z}_{2}}}{2} \right)\)
If P (x1, y1, z1) and Q (x2, y2, z2) be two points, and let R be a point on PQ produced dividing it externally in the ratio m₁ : m₂ (m₁ ≠ m₂). Then the coordinates of R are \(\left( \frac{{{m}_{1}}{{x}_{2}}-{{m}_{2}}{{x}_{1}}}{{{m}_{1}}-{{m}_{2}}},\,\frac{{{m}_{1}}{{y}_{2}}-{{m}_{2}}{{y}_{1}}}{{{m}_{1}}-{{m}_{2}}},\,\frac{{{m}_{1}}{{z}_{2}}-{{m}_{2}}{{z}_{1}}}{{{m}_{1}}-{{m}_{2}}} \right)\)