Vectors – Equation of Straight Line

Vectors – Equation of Straight Line

Equation of Straight Line passing through a given Point and Parallel to a given Vector

Vector Form: Line passing through point \(A(\overline{a})\) and parallel to vector \(\overline{b}\).

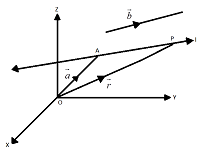
Let A be the given point and let AP be the given line through A.

Let  \(\overline{b}\) be any vector parallel to the given line.

Position vector of point A is \(\overline{a}\).

Let P be any point on line AP, and let its position vector be \(\overline{r}\).

Then, we have

\(\overline{r}=\overline{OP}=\overline{OA}+\overline{AP}\)

\(\overrightarrow{r}=\overrightarrow{a}+\lambda \overrightarrow{b}\) … (1)

Here, \(\overline{r}\) is the position vector of any point P (x, y) on the line. So \(\overrightarrow{r}=x\hat{i}+y\hat{j}+z\hat{k}\).

In, particular, the equation of straight line through origin and parallel to \(\overline{b}\) is \(\overrightarrow{r}=\lambda \overrightarrow{b}\).

Cartesian Form: Let the coordinates of the given point A be (x₁, y₁, z₁) and the direction of the line be a, b and c. Consider the coordinates of any point P be (x, y, z). then

\(\overrightarrow{r}=x\hat{i}+y\hat{j}+z\hat{k}\),

\(\overrightarrow{a}={{x}_{1}}\hat{i}+{{y}_{1}}\hat{j}+{{z}_{1}}\hat{k}\) and

\(\overrightarrow{b}=a\hat{i}+b\hat{j}+c\hat{k}\).

Substituting these values in (1) and equating the coefficients of \(\hat{i},\ \hat{j}\) and \(\hat{k}\). We get

x = x₁ + λa

y = y₁ + λb

z = z₁ + λc

These are parametric equation of the line.

Eliminating the parameter λ, we get \(\frac{x-{{x}_{1}}}{a}=\frac{y-{{y}_{1}}}{b}=\frac{z-{{z}_{1}}}{c}\).

Note:

• Here any point on the line is (x, y, z) ≡ (x₁ + λa, y₁ + λb, z₁ + λc)
• Since the x, y and z – axes pass through the origin and have direction cosine (1, 0, 0), (0, 1, 0) and (0, 0, 1), their equations are
  Equation of x – axis: y = 0, z = 0,
  Equation of y – axis: x = 0, z = 0,
  Equation of z – axis: x = 0, y = 0.