Triangle Law of Vector Addition of Two Vectors

Triangle Law of Vector Addition of Two Vectors

The physical quantities may be broadly classified into the vectors and the scalars. The quantities with magnitude and direction both are known as vector quantities, it means a vector is a physical quantity that has both magnitude and direction. If two non-zero vectors are represented by the two sides of a triangle taken in same order then the resultant is given in opposite order.

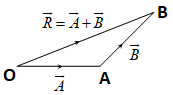
i.e.., \(\overrightarrow{R}=\overrightarrow{A}+\overrightarrow{B}\) \(\because \overrightarrow{OB}=\overrightarrow{OA}+\overrightarrow{AB}\)

1) Magnitude of Resultant Vector:  In ΔABN, \(\cos \theta =\frac{AN}{B}\) ⇒ AN = B cos θ

\(\sin \theta =\frac{BN}{B}\) ⇒ BN = B sinθ; ΔOBN, we have OB² = ON² + BN².

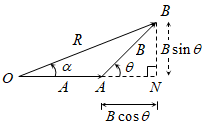
R² = (A + B cosθ)² + (B sinθ)²

R² = A² + B² cos²θ + 2 AB cosθ + B² sin² θ

R² = A² + B² (cos²θ + sin²θ) + 2AB cosθ = A² + B² (1) + 2 AB cosθ

\(R=\sqrt{{{A}^{2}}+{{B}^{2}}+2AB\cos \theta }\).

2) Direction of resultant vectors: If θ is angle between \(\overrightarrow{A}\) and \(\overrightarrow{B}\), then

\(|\overrightarrow{A}+\overrightarrow{B}|\,=\,\sqrt{{{A}^{2}}+{{B}^{2}}+2AB\cos \theta }\) ; If \(\overrightarrow{R}\) makes an angle α with\(\overrightarrow{A}\), then in ΔOBN,

\(\tan \alpha =\frac{BN}{ON}=\frac{BN}{OA+AN}=\frac{B\sin \theta }{A+B\cos \theta }\).