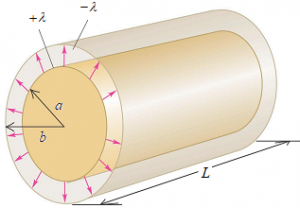
Cylindrical Capacitor
A cylindrical capacitor consists of two coaxial cylinders of radii a and b, say b > a. The outer one is earthed. The cylinders are long enough so that we can neglect fringing of electric fields at the ends. The electric field at a point between the cylinders will be radial, and its magnitude will depend on the distance from the central axis.
Consider a Gaussian surface of length y and radius r such that a < r < b. Flux through the plane surface is zero because the electric field and the area vector are perpendicular to each other.
For the curved part:
\(\phi =\int{\overrightarrow{E}.\overrightarrow{ds}}=\int{Eds}=E\int{ds}=E2\pi ry\),
Consider inside the Gaussian surface is: \(q=\frac{Qy}{L}\),
From Gauss’s law: \(\phi =E2\pi ry=\frac{Qy}{L{{\varepsilon }_{0}}}\),
\(E=\frac{Q}{2\pi {{\varepsilon }_{0}}Lr}\),
Potential difference is: \({{V}_{b}}-{{V}_{a}}=-\int\limits_{a}^{b}{\overrightarrow{E}}.\overrightarrow{dr}=-\int\limits_{a}^{b}{\frac{Q}{2\pi {{\varepsilon }_{0}}Lr}dr}=-\frac{Q}{2\pi {{\varepsilon }_{0}}L}\int\limits_{a}^{b}{\frac{1}{r}dr}\),
\({{V}_{a}}=\frac{Q}{2\pi {{\varepsilon }_{0}}L}\ln \frac{b}{a}\,\,\,\,\,\,\,\,\left( \because \,\,{{V}_{b}}=0 \right)\),
Now, the capacitance is: \(C=\frac{Q}{{{V}_{a}}-{{V}_{b}}}=\frac{Q}{{{V}_{a}}}=\frac{2\pi {{\varepsilon }_{0}}L}{\ln \left( \frac{b}{a} \right)}\).
