Menelaw’s Theorem
Theorem: If a transversal cut the sides BC, CA, AB of a triangle in D, E, F respectively then
BD/DC. CE/EA. AF/FB = -1.
Proof:
Let A (x₁, y₁), B (x₂, y₂) and C (x₃, y₃) be
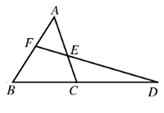
Let the transversal be ax + by + c = 0
BD/DC = The ratio in which ax + by + c = 0 divides BC
= – (ax₂ + by₂ + c)/ (ax₃ + by₃ + c)
CE/EA = The ratio in which ax + by + c = 0 divides CA
= – (ax₃ + by₃ + c)/ (ax₁ + by₁ + c)
AF/FB = The ratio in which ax + by + c = 0 divides AB
= – (ax₁ + by₁ + c)/ (ax₂ + by₂ + c)
Therefore, BD/DC . CE/EA . AF/FB
= – (ax₂ + by₂ + c)/ (ax₃ + by₃ + c) . – (ax₃ + by₃ + c)/ (ax₁ + by₁ + c) . – (ax₁ + by₁ + c)/ (ax₂ + by₂ + c) = -1
