Ceva’s Theorem

Ceva’s Theorem

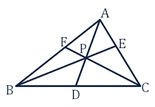
Theorem: If the lines joining any point P, to the vertices A, B, C of a triangle meet the opposite Sides in D, E, F respectively then (BD.CE.AF)/(DC.EA.FB)=1

Proof:

Let A (x₁, y₁), B (x₂, y₂), and C (x₃, y₃) be the vertices.

Let us consider point P is (0, 0)

We know that Slope of AB is (y₂ – y₁)/ (x₂ – x₁) 

A (x₁, y₁) and P(0, 0)

Slope of AP is (y₁ – 0)/ (x₁ – 0)

 = y₁/x₁

Equation of AP is y – 0 = y₁/x₁(x-0)

y  = y₁/x₁(x)

yx₁ = y₁x

⇒ xy₁ – x₁y = 0

BD/DC = -(x₂y₁ – x₁y₂)/(x₃y₁ – x₁y₃)

= (- x₂y₁ + x₁y₂)/(x₃y₁ – x₁y₃)

Slope of BP is (y₂ – 0 )/(x₂ – 0)

= y₂/x₂

Equation of BP is y – 0 =(y₂/x₂)(x – 0)

y =(y₂/x₂)(x – 0)

yx₂ = y₂x

y₂x – yx₂ = 0

CE/EA = -(x₃y₂ – x₂y₃)/(x₁y₂ – x₂y₁)

= (x₂y₃ – x₃y₂  )/(x₁y₂ – x₂y₁)

Slope of CP is y – 0 =y₃/x₃(x – 0)

⇒ x₃y = y₃x

⇒  xy₃ – x₃y = 0

AF/FB = -(x₁y₃ – x₃y₁)/(x₂y₃ – x₃y₂)

= (x₃y₁ – x₁y₃)/(x₂y₃ – x₃y₂)

BD/DC. CE/EA. AF/FB = (- x₂y₁ + x₁y₂)/(x₃y₁ – x₁y₃) . (x₂y₃ – x₃y₂  )/(x₁y₂ – x₂y₁) . (x₃y₁ – x₁y₃)/(x₂y₃ – x₃y₂)

= 1