Specific Heat of Solids
For solids and liquids, we define the specific heat capacity as the quantity of energy that will raise the temperature of unit mass of the body by 1K. When a solid is heated through a small range of temperature, its volume remains more or less constant. Therefore, specific heat of a solid may be called its specific heat at constant volume\({{C}_{V}}\).
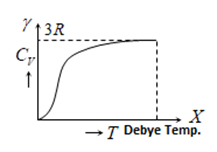
1) From the graph it is clear that at T = 0, \({{C}_{V}}\) tends to zero.
2) With rise in temperature, \({{C}_{V}}\) increases and at particular temperature it becomes constant = 3R = \(6cal/mole\times kelvin=25J/mole\times kelvin\),
3) For most of the solids, Debye temperature is close to room temperature.
4) Dulong and Petit Law: Average molar specific heat of all metals at room temperature is constant, being nearly equal to 3R =\(6\,cal.mol{{e}^{-1}}{{K}^{-1}}=25J.mol{{e}^{-1}}{{K}^{-1}}\), where R is gas constant for one mole of the gas. The statement is known as Dulong and Petiti law.
5) Debey’s law: It was observed that at very low temperature molar specific heat\(\propto \,{{T}^{3}}\).
6) Specific heat of ice: In C.G.S system, \({{C}_{ice}}=0.5\frac{cal}{gm\times {}^{0}C}\).
In S.I system, \({{C}_{ice}}=500\frac{cal}{kg\times {}^{0}C}=2100\frac{Joule}{kg\times {}^{0}C}\),
Solids have only one specific heat but whereas for fluids have two specific heats i.e., specific heat at constant pressure and specific heat at constant volume, because solids are very insensitive to change in volume under the application of external pressure.
