Energy Density in a Parallel Plate Capacitor
Energy density is the total energy per unit volume of the capacitor as the electrostatic energy stored in a parallel plate capacitor is U = ½ CV².
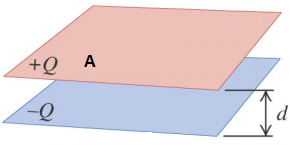
Where, for a parallel plate capacitor, \(C=\frac{{{\varepsilon }_{0}}A}{d}\) and V = Ed; so,
\(U=\frac{1}{2}\left( \frac{{{\varepsilon }_{0}}A}{d} \right){{\left( Ed \right)}^{2}}=\frac{1}{2}{{\varepsilon }_{0}}{{E}^{2}}\left( Ad \right)\),
Where Ad = Volume of the capacitor (V). Then
\(\frac{U}{V}=\frac{dU}{dV}\), that is the energy stored per unit volume can be given by:
\(\frac{dU}{dV}\left( {{u}_{V}} \right)=\frac{1}{2}{{\varepsilon }_{0}}{{E}^{2}}\).
Although we have proved the above result for a parallel plate capacitor, in general, this is true for any kind of capacitor or any kind of electric field. The potential energy of a spherical capacitor made of a single sphere can be found using the concept of energy density. Energy density is given by:
u = ½ ε₀E²,
\(dU=u\,dV=\frac{1}{2}{{\varepsilon }_{0}}{{\left( \frac{1}{4\pi {{\varepsilon }_{0}}}\frac{Q}{r} \right)}^{2}}4\pi {{r}^{2}}dr\),
∴ \(U=\frac{1}{8\pi {{\varepsilon }_{0}}}{{Q}^{2}}\int\limits_{R}^{\infty }{\frac{dr}{{{r}^{2}}}}=\frac{{{Q}^{2}}}{8\pi {{\varepsilon }_{0}}R}\).
