Multiplication of a Vector by a Scalar
Let \(\overline{a}\) be a vector and λ a scalar. Then the product of vector \(\overline{a}\) by scalar λ, denoted by \(\lambda \overline{a}\), is called the multiplication of vector by the scalar λ.
Note that \(\lambda \overline{a}\) is also a vector, collinear to vector \(\overline{a}\). Vector \(\lambda \overline{a}\) has the direction same (or opposite) as that of vector \(\overline{a}\) if the value of λ is positive (or negative). Also, the magnitude of vector \(\lambda \overline{a}\) is |λ| time the magnitude of vector \(\overline{a}\) , i. e.,
\(\left| \lambda \overline{a} \right|=\left| \lambda \right|\left| \overline{a} \right|\).
A geometric visualization of multiplication of a vector by a scalar is given in the following figure.
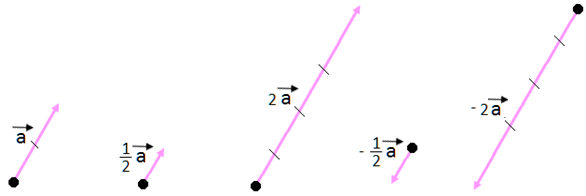
When \(\lambda =-1,\ \lambda \overline{a}=-\overline{a}\), which is a vector having magnitude equal to the magnitude of \(\overline{a}\) and direction opposite to that of the direction of \(\overline{a}\).
Vector \(-\overline{a}\) is called the negative (or additive inverse) of vector \(\overline{a}\) .
\(\overline{a}+(-\overline{a})=\left( \overline{-a} \right)+\overline{a}=0\).
Also, if \(\lambda =\frac{1}{\left| \overline{a} \right|}\), provided \(\overline{a}\ne 0\) i.e., \(\overline{a}\) is not a null vector, then
\(\left| \lambda \overline{a} \right|=\left|
\lambda \right|\left| \overline{a}
\right|=\frac{1}{\left| \overline{a} \right|}\times \left| \overline{a}
\right|=1\).
Example: Find a vector in the direction of vector \(5\overline{i}-\overline{j}+2\overline{k}\) which has magnitude 8 units
Solution:
Given that \(5\overline{i}-\overline{j}+2\overline{k}\),
Let \(\overline{a}=5\overline{i}-\overline{j}+2\overline{k}\),
\(\left| \overline{a} \right|=\sqrt{{{5}^{2}}+{{(-1)}^{2}}+{{2}^{2}}}\),
\(=\sqrt{25+1+4}=\sqrt{30}\).
\(\widehat{a}=\frac{\overrightarrow{a}}{\left| \overrightarrow{a} \right|}\),
\(=\frac{5\overline{i}-\overline{j}+2\overline{k}}{\sqrt{30}}\).
Hence, the vector in the direction of vector \(5\overline{i}-\overline{j}+2\overline{k}\) which has magnitude 8 units is given by
\(8\widehat{a}=8\left( \frac{5\overline{i}-\overline{j}+2\overline{k}}{\sqrt{30}} \right)\),
\(=\frac{40}{\sqrt{30}}\overline{i}-\frac{8}{\sqrt{30}}\overline{j}+\frac{16}{\sqrt{30}}\overline{k}\).
