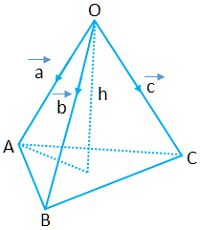
Volume of Tetrahedron Tetrahedron is a pyramid having a triangular base. Therefore, Volume = ⅓ [(Height) x (Area of base)] , , Now h is projection of on vector which is normal to the plane. Vector normal to the plane ABC is . Therefore, , , Volume , . Share Tweet View Email Print Follow
Vectors Algebra – Sine Rule Sine Rule: If A, B and C are the vertices of a triangle ABC, then sine rule , Let , , , So that , Therefore , , , , , , , , , Dividing both sides by abc, we get , . . .(1) , . Read more about Vectors Algebra – Sine Rule[…]
Cosine Rule Using Dot Product Using vector method, prove that in a triangle . (Cosine law) In Triangle ABC, Let Since Squaring on both sides (since angle between and = angle between CA produced and AB) Example: Find the angle between the vectors and . Solution Given that . = 1.3 + (-2) (-2) Read more about Cosine Rule Using Dot Product[…]
Auxiliary Circle and Eccentric Angle A Circle described on the major axis as diameter is called the Auxiliary Circle. For the Ellipse , (a > b) it has equation x² + y² = a². P ≡ (a cos θ, b sin θ) Q ≡ (a cos θ, a sin θ), a ≤ θ ≤ 2π Read more about Auxiliary Circle and Eccentric Angle[…]
Inequalities Involving Absolute value (i) |x| ≤ a (where a > 0) It implies those value of x on real number line which are at distance a or less than a from zero. ⇒ -a ≤ x ≤ a Examples: |x| ≤ 2 ⇒ -2 ≤ x ≤ 2 |x| < 3 ⇒ -3 < Read more about Inequalities Involving Absolute value[…]
Intersection of a Line and Hyperbola Equation of line is y = mx + c . . . (1) and equation of hyperbola is x²/a² – y²/b² = 1 . . . (2) from equation (1) and (2) b²x² – a² (mx + c) ² = a² b² (b² – a²m²) x² – 2a²mcx – Read more about Intersection of a Line and Hyperbola[…]
Equation of a Hyperbola referred to Two Perpendicular Lines Consider the hyperbola . From figure Let P (x₁, y₁) be any point on the hyperbola. Then, PM = y and PN = x Therefore, . If the perpendicular distances P₁ and P₂ of a moving point P (x, y) from two mutually perpendicular coplanar straight Read more about Equation of a Hyperbola referred to Two Perpendicular Lines[…]
Circle – Director Circle and Its Equation Director Circle: The locus of the point of intersection of two perpendicular tangents to given circle is known as Director Circle. Equation of Director Circle: Method (1): The equation of any tangent to the circle x² + y² = a² is y = mx + a √ (1 Read more about Circle – Director Circle and Its Equation[…]
Equation of the Parabola when Vertex is (h, k) and Axis is Parallel to X – axis and Y – axis Equation of the Parabola when Vertex is (h, k) and Axis is Parallel to X – axis: The parabola y² = 4ax Can be written as (y – 0)² = 4a(x – 0) … Read more about Equation of the Parabola when Vertex is (h, k) and Axis is Parallel to X – axis and Y – axis[…]
Pair of Straight Lines – Homogeneous Second Degree Equation An equation (whose RHS is zero) in which the sum of the power of x and y in every term is the same say n, is called a Homogeneous equation of nth degree in x and y. Thus, ax² + 2hxy + by² = 0 is Read more about Pair of Straight Lines – Homogeneous Second Degree Equation[…]