Circle – Director Circle and Its Equation

Circle – Director Circle and Its Equation

Director Circle: The locus of the point of intersection of two perpendicular tangents to given circle is known as Director Circle.

Equation of Director Circle:

Method (1): The equation of any tangent to the circle

x² + y² = a² is y = mx + a √ (1 + m²) … (1)

Let P (h, k) be the point of intersection of the tangents. Then P (h, k) lies on (1).

k = m h + a √ (1 + m²)

k – m h = a √ (1 + m²)

Squaring on both sides

(k – m h)² =  a²(1 + m²)

k² + m²h² – 2mkh = a² + m²a²

Let two roots be m₁ and m₂.

The tangent perpendicular distance

m₁ m₂ = -1

(k² – a²)/(h² – a²) = -1

k² – a² = -h² + a²

h² + k² = 2a²

Hence, the locus of P (h, k) is x² + y² = 2 a².

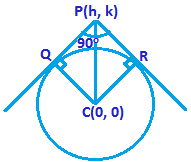
Method (2): From figure, CRPQ is a square, therefore

CQ = CP cos 45⁰

2a² = h² + k²

x² + y² = 2a²

Which is required locus.

Note: The equation of director circle for the circle (x – h) ² + (y – k) ² = a² is given by (x – h) ² + (y – k) ² = 2a².

Example: Find the equation of director circle for the circle x ² + y ² = 16.

Solution: Given that

x ² + y ² = 16

x ² + y ² = 4²

a = 4

The equation of director circle is x ² + y ² = 2(4)

x ² + y ² = 8.