Auxiliary Circle and Eccentric Angle

Auxiliary Circle and Eccentric Angle

A Circle described on the major axis as diameter is called the Auxiliary Circle. For the Ellipse \(\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\), (a > b) it has equation x² + y² = a².

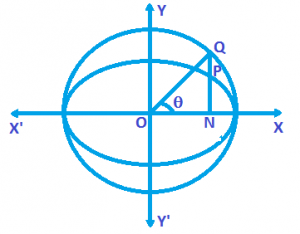
P ≡ (a cos θ, b sin θ)

Q ≡ (a cos θ, a sin θ), a ≤ θ ≤ 2π

Here, θ is called the Eccentric angle of point P, P and Q are the corresponding points and θ is called the eccentric angle of point P.

\(\frac{PN}{PQ}=\frac{b\ \sin \theta }{a\sin \theta -b\sin \theta }=\frac{b}{a-b}\) = Constant

Hence, if from each point on a circle, perpendicular are drawn on a fixed diameter, then the locus of a point P dividing these perpendiculars in a constant ratio is an ellipse whose auxiliary circle is the original circle.

Example: Find the equation of the curve whose parametric equation are x = 1 + 4 cos θ, y = 2 + 3 sin θ, θ ϵR.

Solution: Given that   x = 1 + 4 cos θ,

y = 2 + 3 sin θ

x = 1 + 4 cos θ

x – 1 = 4 cos θ

(x – 1)/4 = cos θ

Squaring on both sides

(x – 1)²/16 = cos² θ … (1)

y = 2 + 3 sin θ

y – 2 = 3 sin θ

(y – 2)/3 = sin θ

Squaring on both sides

(y – 2)²/9 = sin² θ….(2)

Equation (1) + (2)

(x – 1)²/16  + (y – 2)²/9  = cos² θ + sin² θ

(x – 1)²/16  + (y – 2)²/9 = 1

Which is an Ellipse.