Equation of the Parabola when Vertex is (h, k) and Axis is Parallel to X – axis and Y – axis

Equation of the Parabola when Vertex is (h, k) and Axis is Parallel to X – axis and Y – axis

Equation of the Parabola when Vertex is (h, k) and Axis is Parallel to X – axis:

The parabola y² = 4ax

Can be written as (y – 0)² = 4a(x – 0) … (1)

The vertex of this parabola is A (0, 0)

Now, when the origin is shifted to A’ (h, k) without changing the direction of the axes.

The equation becomes (y – k)² = 4a(x – h) … (2)

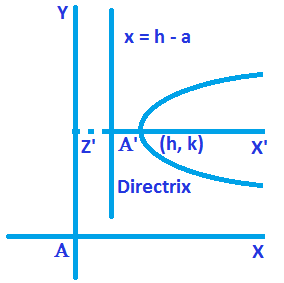
This is called the general form of the parabola (1) and axis A’X’ || AX with its vertex at A’ (h, k).

Its focus is at (a + h, k) and the length of latus rectum is 4a.

The equation of the directrix is

x = h – a

x + a – h = 0

Equation of the Parabola when Vertex is (h, k) and Axis is Parallel to Y – axis:

The parabola x² = 4ay

Can be written as (x – 0)² = 4a(y – 0) … (1)

The vertex of this parabola is A (0, 0)

Now, when the origin is shifted to A’ (h, k) without changing the direction of the axes.

The equation becomes (x – h)² = 4a (y – k) … (2)

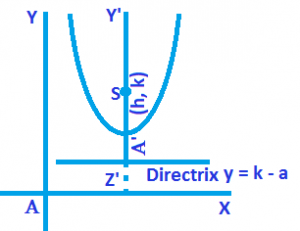
Its vertex at A’ (h, k).

Its focus is at (h, a + k) and the length of latus rectum is 4a.

The equation of the directrix is

y = k – a

y + a – k = 0

Example: Find the value of p such that the vertex of y = x² + 2px + 13 is 4 units above the x – axis.

Solution: Given parabola is  y = x² + 2px + 13

y = (x + p)² – p²  + 13

y – (13 -p²) = ( x + p) ²                                                             

So, the vertex is (-p, 13-p²)

Since, the parabola is at a distance of 4 units above the x – axis

13 – p² = 4

⇒ p² = 13 – 4

⇒ p² = 9

⇒ p = ± 3.