Intersection of a Line and Hyperbola
Equation of line is y = mx + c . . . (1)
and equation of hyperbola is x²/a² – y²/b² = 1 . . . (2)
from equation (1) and (2)
b²x² – a² (mx + c) ² = a² b²
(b² – a²m²) x² – 2a²mcx – a² (b² + c²) = 0 . . . (3)
Hence y = mx ± √ (a²m² – b²) is a tangent to the standard hyperbola.
In this equation of tangent.
a²m² – b² ≥ 0
m² ≥ b²/a²
m ϵ (-∞, -b/a] È [b/a, ∞)
Hence, for given m, there can be two parallel tangents to the hyperbola.
If the tangents pass through (h, k), then
(k – m h) ² = a²m² – b²
(h² – a²) m² – 2kmh + k² + b² = 0
Hence, passing through a given point (h, k), there can be maximum of two tangents. Now
m₁ + m₂ = 2kh/ (h² – a²) . . . (4)
m₁ m₂ = (k² + b²)/ (h² – a²) . . . (5)
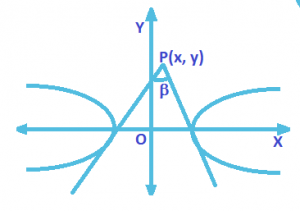
β is the angle enclosed by the tangent as shown in figure.
Now
tan²β = ((m₁ + m₂)² – 4m₁m₂) / (1 + m₁ m₂) . . . (6)
Equation (4) and (5) substitute in equation (6).
If β = 90⁰, the m₁ m₂ = -1
Hence, from (5), we get
k² + b² = a² – h²
x² + y² = a² – b²
which is the equation of the director circle of the hyperbola.
- If a > b the director circle is real is a point with finite radius.
- If a = b, the director circle is a point circle which is the origin
- If a < b, there no real circle or no such point on the plane.
Note:
For hyperbola (x – h)²/a² – (y – k) ²/b² = 1, the equation of tangent at point P(x₁, y₁) is
y – y₁ = m(x – x₁) ± √(a²m² – b²).
Example: For all real values of m, the straight-line y = mx + 6 is a tangent to the hyperbola
x²/ 100 – y²/49 = 1.
Solution: Given that
straight-line y = mx + 6 and
hyperbola x²/ 100 – y²/49 = 1.
c² = a²m² – b²
c = 6, a² = 100 and b² = 49
Therefore, 36 = 100m² – 49
100m² = 85
m = √ (17/20)
