Young’s double slit Experiment
Young’s interference experiment, also called Young’s double-slit interferometer, was the original version of the modern double-slit experiment, performed at the beginning of the nineteenth century by Thomas Young. This experiment played a major role in the general acceptance of the wave theory of light. Young’s double slit experiment uses two coherent sources of light placed at a small distance apart, usually only few orders of magnitude greater than the wavelength of light is used.
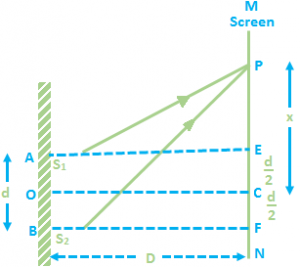
Let A and B be two fine slits, a small distance d apart. Let them be illuminated by a monochromatic light of wavelength l. MN in the screen is at a distance D from the slits AB. The waves from A and B superimpose upon each other and an interference pattern is obtained on the screen. The point C is equidistant from A and B and therefore the path difference between the waves will be zero and so the point C is of maximum intensity. It is called the central maximum.
For another point P at a distance ‘x’ from C, the path difference at P = BP – AP.
Now AB = EF = d, AE = BF = D
ΔBPF (Using Pythagoras Theorem):
BP² = [BF² + PF²]½ = \({{\left[ {{D}^{2}}\,+\,{{\left( x\,+\,\frac{d}{d} \right)}^{2}} \right]}^{1/2}}\,=\,D{{\left[ 1\,+\,\frac{{{\left( x+\frac{d}{2} \right)}^{2}}}{{{D}^{2}}} \right]}^{1/2}}\)
Similarly in ΔAPE:
\(AP\,=\,D\,{{\left[ 1\,+\,\frac{{{\left( x\,-\,\frac{d}{2} \right)}^{2}}}{{{D}^{2}}} \right]}^{1/2}}\)
∴ BP – AP = \(D\left[ 1+\frac{1}{2}\frac{{{\left( x+\frac{d}{2} \right)}^{2}}}{{{D}^{2}}} \right]\,-\,D\left[ 1\,+\,\frac{1}{2}\frac{{{\left( x\,-\,\frac{d}{2} \right)}^{2}}}{{{D}^{2}}} \right]\)
After expanding the above equation binomially,
\(BP\,-\,AP=\,\frac{1}{2D}\,\left[ 4\times \frac{d}{2} \right]\,=\,\frac{xd}{D}\)
For bright fringes (constructive wavelength) the path difference is integral multiple of wavelength i.e., path difference is nλ.
∴ \(n\lambda \,=\,\frac{xd}{D}\)
⇒ \(x\,\,=\,\,\frac{n\lambda D}{d}\)
Where, n = 0, 1, 2, 3, 4 …
(x therefore represents distance of nth bright fringe from C)
Now,
∴ n = 0 x₀ = 0
n = 1 \({{x}_{1}}\,=\,\frac{\lambda D}{d}\)
n = 2 \({{x}_{2}}\,=\,\frac{2\lambda D}{d}\)
n = 3 \({{x}_{3}}\,=\,\frac{3\lambda D}{d}\)
And so on.
\({{x}_{1}}\,=\,\frac{\lambda D}{d}\) is the distance of the 1st bright fringe and therefore
\({{x}_{n}}\,=\,\frac{n\lambda D}{d}\) will be the distance of the nth bright fringe from C.
Therefore, separation between the centres of two consecutive bright fringe is the width of a dark fringe.
∴ β₁ = xn – xn₋₁ = \(\frac{\lambda D}{d}\)
Similarly for dark fringes,
xn = (2n – 1) \(\frac{\lambda D}{2d}\)
For n = 1, \({{x}_{1}}\,=\,\frac{\lambda D}{2d}\) → Position of 1st dark fringe.
For n = 2, \({{x}_{2}}\,=\,\frac{3\lambda D}{2d}\) → Position of 2nd dark fringe.
The separation between the centres of two consecutive dark interference fringes is the width of a bright fringe.
∴ β₂ = xn – xn₋₁ =\(\frac{\lambda D}{d}\)
The separation between the centres of two consecutive dark interference fringes is the width of a bright fringe. All bright and dark fringes are equal width as b₁ = b₂.
