Permutations
Each of the different arrangements which can be made by taking some or all of a number of distinct objects is called a permutation. If n is a natural number and r is a positive integer satisfying 1 ≤ r ≤ n then the natural number \(\frac{n!}{\left( n-r \right)!}\) is denoted by the symbol ⁿPr or P (n, r).
ⁿPr = P (n, r) = \(\frac{n!}{\left( n-r \right)!}\).
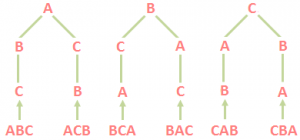
Consider the set {a, b, c} of first three letters of the English alphabet various combinations (selections) of these three letters taken two at a time are as follows.
ab, bc, ca
Here selection ab is same as ba similarly selection bc and ca are same as cb and ac respectively.
Now if we want to list all the possible arrangements of these three letters taking two at a time then letters in each of the above selections, will be arranged and we will obtain following arrangements.
ab bc ca
ba cb ac
Example: Let r and n be positive integers such that 1 ≤ r ≤ n. Then the number of all permutations of n distinct items or objects taken r at a time is n (n – 1) (n – 2) … (n – (r – 1)).
= \(\frac{n\left( n-1 \right)\left( n-2 \right)…..\left( n-\left( r-1 \right) \right)\left( n-r \right)!}{\left( n-r \right)!}\),
= \(\frac{n!}{\left( n-r \right)!}\),
= ⁿPr
The number of all permutations (arrangements) of n distinct objects taken all at a time is n!.
Examples:
1. ⁵P₂ = P (5, 2)
= \(\frac{5!}{\left( 5-2 \right)!}=\frac{5!}{3!}=\frac{5\times 3\times 2\times 1}{3\times 2\times 1}\) = 20.
2. ⁴P₄ = P (4, 4) = \(\frac{4!}{\left( 4-4 \right)!}=\frac{4!}{0!}\) = 4! = 24
3. ⁿPn = \(\frac{n!}{\left( n-n \right)!}=\frac{n!}{0!}\) = n!
4. ⁿPₒ = \(\frac{n!}{\left( n-0 \right)!}=\frac{n!}{n!}\) = 1
Permutations under certain Conditions: The number of all permutations (arrangements) of n different objects taken r at a time.
- When a particular object is to be always included in each arrangement is ⁿ⁻¹Cr₋₁ x r!
- When a particular object is to never taken in each arrangement is ⁿ⁻¹Cr x r!
- When a particular object is to be always occur together is ⁿ⁻²Cr₋₂ x (r – 1)! x r!
Examples:
1. How many numbers of five digits can be made with at least one replaced digit?
Solution: Total number of five digit numbers = 9 x 10 x 10 x 10 x 10 = 90000.
And total number of five digit numbers with district digits.
= (¹⁰C₅ x 5! – ⁹C₄ x 4!)
= 27216
Hence, the required number of numbers having at least one repeated digit.
= 90000 – 27216
= 62784
2. Here are ten chairs in a row. In how many ways can two people be seated?
![]()
Solution: Suppose there were only 3 chairs. The two persons A and B can be seated in six different arrangements.

The first person to sit has three choices where he wants to sit on. After having chosen the chair, the second person has only two chairs to choose from. By the multiplication principle, the two people can sit in 3 x 2 = 6 different arrangements.
For ten chairs, the number of distinct arrangement of two people in a row of 10 chairs is P (10, 2) = 10!/ 8! = 90.
The first person has 10 chairs to choose from and having chosen it the second person 9 choices left. By the multiplication principle the number of arrangements is 10 × 9 = 90.
