The Work Energy Theorem is the Idea that energy and work can be directly exchanged for one another. For example, if you do three joules of work to get a bowling ball moving, it is now moving with three joules of kinetic energy.
According to the principle, work done by a force in displacing a body, gives the measure of the change in kinetic energy of the body.
When a force does some work on a body, the kinetic energy of the body increases by the same amount. Conversely, when an opposing force is applies on a body, its kinetic energy decreases. The decrease in kinetic energy is equal to the work done by the body against the retarding force. Thus, work and kinetic energy are equivalent quantities.
Suppose,
m = mass of a body
u = initial velocity of the body
\(\overrightarrow{F\,}\) = Force applied on the body in direction of motion
\(\overrightarrow{ds}\) = Small displacement of the body in the direction of \(\overrightarrow{F\,}\)
Here, the small amount of work done by the force is,
\(\overrightarrow{dW}\) = F.ds = F ds cosθ = F ds
dW = F ds
= (ma) ds (∵ F = ma)
\(=\,\,m\,\left( \frac{dv}{dt} \right)\,ds\,\,\,\,\,\,\,\,\left( \because \,a\,=\,\frac{dv}{dt} \right)\)
\(=\,m\,\left( \frac{ds}{dt} \right)\,dv\,\)
dW = mvdv \(\left( \because \,\,v=\,\frac{ds}{dt} \right)\)
Total work done by the force in increasing the velocity of the body from u to v
\(W\,=\,\int\limits_{u}^{v}{mv\,dv}\,=\,m\,{{\left[ \frac{{{v}^{2}}}{2} \right]}^{v}}_{u}\) = ½ m (v² – u²)
W = ½ mv² – ½ mu² = (K.E)initial – (K.E)final
W = (K.E)initial – (K.E)final
W = Change in the kinetic energy of the body.
For Example consider the following figure: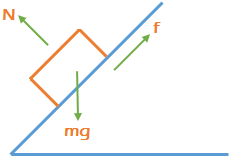 According to the work energy theorem,
According to the work energy theorem,
Work done by all the force = Change in Kinetic Energy
Wg + WN + Wf = Kf – Ki
Wg = Work done by gravity
WN = Work done due to Normal force
Wf = Work done by friction
Kf = Final Kinetic Energy
Ki = Initial Kinetic Energy
How to find the Work Energy Theorem?
Example: A 0.600 kg particle has a speed of 2 m/sec at point A and kinetic energy of 7.50 J at point B. what is (a) its kinetic energy at A? (b) Its speed at B? (c) The total work done on the particle as it moves from A to B?
Solution: Given,
m = 0.600 kg
VA = 2 m/sec
KB = 7.50 J
a) KA = ½ mVA²
KA = ½ (0.600 kg) (2 m/sec)²
KA = 1.20 J
b) KB = ½ mVB²
7.50 J = ½ (0.600 kg) VB²
\({{V}_{B}}^{2}\,=\,\frac{7.50\,J}{0.300\,kg}\)
VB = 5 m/sec
c) WA→B = ΔK = KB – KA
= 7.50 – 1.20
= 6.30 J
