In the 18th century Daniel Bernoulli noticed that fluids flow faster when forced through constrictions. We usually come across these kinds of phenomenon when we observe and compare rapids and meandering rivers.
Bernoulli reasoned that when a particular energy increases in a system the rest of the forms of energy must decrease.
To understand this principle the best example would be observing the lifting of an airplane. An airplane wing is shaped in such a way that the air passing over it must travel further and faster than the air passing underneath. This leads to a lower air pressure build up on the wing than the air below. This produces the lift force which keeps the airplane afloat.
Bernoulli’s Principle Definition: This principle basically gives us a relation between velocity, pressure and height of the following non viscous fluid in a horizontal flow.
According to it, the speed and pressure of the flowing fluid are inversely proportional to each other, that is, if the velocity increases, it will lead to an automatic decrease in the pressure of the fluid.
We can also say that, the theorem states that for the streamline flow of an ideal liquid, the total energy (sum of pressure energy, potential energy and kinetic energy) per unit mass remains constant at every cross- section, throughout the flow.
Hence according to this principle, for a horizontal flow, if the velocity increases then the pressure exerted by the fluid will decrease.
Bernoulli’s Principle Equation: This theorem is a consequence of the principle of conservation of energy, applied to ideal liquid in motion. As per the theorem statement that is for the streamline flow of an ideal liquid, the total energy per unit mass remains constant at every cross section, throughout the flow.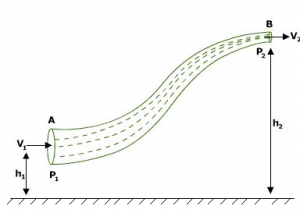
Consider a tube AB of varying cross section and at different heights. Let an ideal liquid (an ideal liquid is incompressible and non-viscous) flow through it in a streamline. Since the liquid is flowing from A to B is p₁ > p₂.
Now,
A₁v₁r = A₂v₂r = m (∵ Equation of continuity)
Here, A₁ > A₂. So, v₁ < v₂
The force on the liquid at A = ρ₁A₁ and the force on the liquid at B = ρ₂A₂.
Now, the work done per second on the liquid at section,
A = r₁A₁v₁
= ρ₁v₁
Where v₁ is the velocity and V₁ is Volume of liquid per sec.
Here, \(\frac{work\,done}{\sec }\,\,=\,\,force\,\,\times \,\,\frac{dis\tan ce}{time}\,\,\,=\,\,\,force\,\,\times \,\,velocity\)
Now, the work done per second on the liquid at section,
B = ρ₁A₁v₂
= ρ₂v₂
Since, V₁ = V₂ = V (Equation of Continuity)
Net work done per second on the liquid by the pressure energy in moving from A to B = ρ₁v – ρ₂v.
The net work done per second, in turn, increases the P.E per second and also increases the K.E per sec, from A to B. This is in accordance with the laws of conservation of energy.
\({{p}_{1}}v\,-\,{{p}_{2}}v\,=\,(mg{{h}_{2}}\,-\,mg{{h}_{2}})\,+\,\left(\frac{1}{2}m{{v}_{2}}^{2}\,-\,\frac{1}{2}m{{v}_{1}}^{2} \right)\)
\({{p}_{1}}v\,+\,mg{{h}_{1}}\,+\,\frac{1}{2}m{{v}_{1}}^{2}\,=\,{{p}_{2}}v+mg{{h}_{2}}+\frac{1}{2}m{{v}_{2}}^{2}\)
\(\frac{{{p}_{1}}v}{m}+g{{h}_{1}}+\frac{1}{2}{{v}_{1}}^{2}=\,\frac{{{\rho}_{2}}v}{m}+g{{h}_{2}}+\frac{1}{2}{{v}_{2}}^{2}\)
\(\frac{{{p}_{1}}}{\rho }+g{{h}_{1}}+\frac{1}{2}{{v}_{1}}^{2}=\frac{{{p}_{2}}}{\rho }+g{{h}_{2}}+\frac{1}{2}{{v}_{2}}^{2}\)
\(\frac{p}{\rho }+gh+\frac{1}{2}{{v}^{2}}\,\,=\,\operatorname{Co}ns\tan t\)
Summation of pressure energy per unit mass and Potential energy per unit mass and Kinetic energy per unit mass is constant for streamline flow of an ideal liquid.
Examples of Bernoulli’s Principle:
- Air Plane Lift: The wings of the plane are designed in such a manner that the air flowing under the wings moves at a speed which is greater than that of the upper part. Hence it results into a difference in pressure such that the pressure exerted is more upwards than in downwards direction. This results in a lift.
- Venturi meter: It is a device that is used to measure the rate of flow of a liquid through a pipe. It has three parts: a short converging pipe, a throat and a diverging part as well.
- Pilot tube: It is a device used for measuring the velocity of flow at any point in a pipe or a channel. It is based on the principle that if the velocity of flow at a point becomes zero, the pressure there is increased due to the conversion of the kinetic energy into pressure energy.
- The spoiler of the race car is shaped in a way to obtain the maximum speed during the race.
- Race cars also use this Bernoulli’s principle to keep the wheel pressed to the racing track.