A quantity that has magnitude as well as direction is called a vector. A directed line segment is a vector.
The point A from where the vector AB starts is called its initial point, and the point B where it ends is called its terminal point. The distance between initial and terminal points of a vector is called the magnitude (or length) of the vector. The arrow indicates the direction of the vector.
Example:
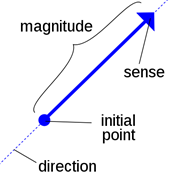Position Vector: Position vector is the vector which represents the position of a point in a space with respect to the origin O. It also represents the distance and direction of the points from the origin. If P is the point.
Position vector of a point P(x, y, z) is given as OP = (r) = xi + yj + zk, and its magnitude by \(\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}\) . This form of any vector is called its component form. x, y and z are called as the scalar components.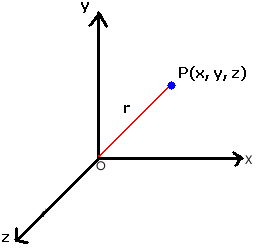
Type of Vectors
Zero Vector: A zero vector, denoted, is a vector of length 0, and thus has all components equal to zero. It is the additive identity of the additive group of vectors.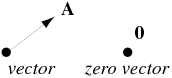
Unit Vector: A vector whose magnitude is unity (1 unit) is called a unit vector.
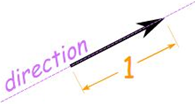Co-initial Vectors: Two or more vectors having the same initial point are called coinitial vectors.
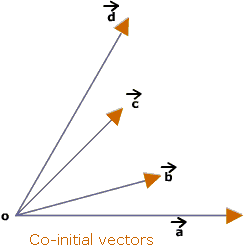Collinear Vectors: Two or more vectors are said to be collinear if they are parallel to the same line, irrespective of their magnitudes and directions.
Equal Vectors: Two vectors are said to be equal, if they have the same magnitude and direction regardless of the positions of their initial points.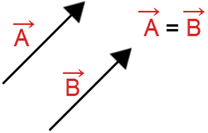
Negative of a Vector: A vector whose magnitude is the same as that of a given vector, but direction is opposite to that of it, is called negative of the given vector.
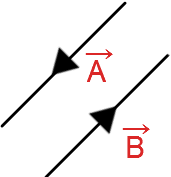Addition of Vectors: If we have two vectors with the same direction, then the addition of them is equal to the sum of their magnitude and will has the same direction.
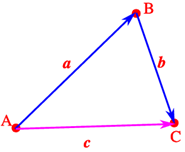
If we have two vectors with different direction, then vector addition can take place by triangle law or parallelogram law.
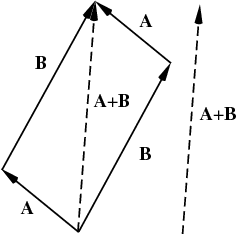Triangle Law of Vector Addition: If we have two vectors, then to add them, they are positioned so that the initial point of one coincides with the terminal point of the other.