We know that hot water of milk, when kept at room temperature, cool drown gradually. But have you noticed that the rate at which hot milk cools down to a lukewarm state is lesser as compared to that required by a lukewarm milk to cool and attain the room temperature? Have you ever wondered why this happens? In this section, we will learn about Newton’s Law of Cooling which provides the explanation for this behaviour.
What is Newton’s Law of Cooling?
Newton’s law of cooling states that the rate of cooling of a body is directly proportional to the temperature difference between the body and the surroundings. The law holds good only for a small difference of temperature. Loss of heat by radiation depends on the nature of the surface and the area of the exposed surface.
Expression for Newton’s Law of Cooling: According to Newton’s law of cooling the rate of loss of heat, \(-\,\frac{dQ}{dt}\) of the body is directly proportional to the difference of temperature ΔT = (T₂ – T₁) of the body and the surroundings. The law holds good only for small difference of temperature. Also the loss of heat by radiation depends upon the nature of the surface of the body and the area of the exposed surface. We can write,
\(-\,\frac{dQ}{dt}\,=\,k({{T}_{2}}\,-\,{{T}_{1}})\),
Where, K is the Positive Constant depending upon the area and nature of the surface of the body. Suppose a body of mass m and specific heat “s” is at temperature T₂. Let T₁ be the temperature falls by a small amount dT₂ in time dt, then the amount of heat lost is, dQ = msdT₂.
Therefore, rate loss of heat is given by
\(\frac{dQ}{dt}\,=\,ms\frac{d{{T}_{2}}}{dt}\).
From equations we have,
\(-\,ms\frac{d{{T}_{2}}}{dt}\,=\,k({{T}_{2}}\,-\,{{T}_{1}})\),
\(\frac{dT}{{{T}_{2}}\,\,-\,\,{{T}_{1}}}\,=\,-\,\frac{k}{ms}dt\,=\,-\,Kdt\),
Where,
K = k/ms
On Integrating,
loge (T₂ – T₁) = -Kt + c
T₂ = T₁ + C’ e-Kt, Where C’ = ec.
From the equation above, we can see that the nature of graph obtained for temperature with respect to time is exponential in nature, as can be seen in the plot below. Here we notice that the cooling of fluid depends on the difference of its temperature and the surrounding. The plot for the rate of change of temperature is steeper in the beginning and as the temperature decreases with time, it becomes gradual, hence the rate of cooling is higher at the beginning and decreases as the temperature of the body falls.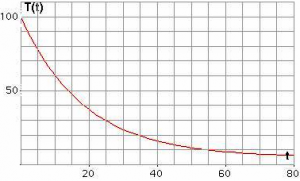
This plot can be derived experimentally using the setup shown in the figure below. Here we take some water in calorimeter with the proper stirring mechanism and cover it with a lid consisting of two holes through which a thermometer is dipped in the fluid.
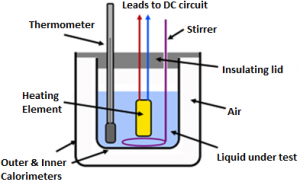The water is heated till it reaches a temperature of 400C. The heat source is then removed the system is left for cooling and the stopwatch is then started. The reading of the thermometer and the stopwatch is noted at regular intervals. As the water reaches the room temperature, we stop the experiment. As we plot the temperature on the Y – axis and the time on the X – axis, we get a graph similar to that shown above.
How to find the Newton’s Law of Cooling?
Problem: Robin heats the water to 700C. He waits for 10 min. How much would be the temperature if K = 0.56 per min and Surrounding temperature is 270C?
Solution: Given,
Ts = 27⁰ C
T0 = 70⁰ C
t = 10 min
K = 0.56
Using Newton’s Law of Cooling:-
T (t) = Ts + (T0 – Ts) e-Kt
= 27 + (70 – 27) e-(0.56)
= 27 + 24.56
= 51.56⁰ C
Therefore, the temperature cools down from 70⁰ C to 51.56⁰ C after 10 mins.