Solution of Triangles – Part 1

Solution of Triangles – Part 1

The three sides a, b, c and the three angles A, B, C are called the elements of the triangle ABC, when any three of these six elements(except all three angles) of a triangle are given, the triangle is know as completely that is the  other three elements and can be expressed in terms of the given elements and can be evaluated. This process is called the solution of triangles.

(i) If the three sides a, b and c are given, angle A is obtained from

  \(\tan \frac{A}{2}=\sqrt{\frac{\left( s-b \right)\left( s-c \right)}{s\left( s-a \right)}}\) (or) \(\cos A=\frac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}\)

\(\tan \frac{B}{2}=\sqrt{\frac{\left( s-a \right)\left( s-c \right)}{s\left( s-b \right)}}\)  (or) \(\cos B=\frac{{{a}^{2}}+{{c}^{2}}-{{b}^{2}}}{2ac}\)

\(\tan \frac{C}{2}=\sqrt{\frac{\left( s-a \right)\left( s-b \right)}{s\left( s-c \right)}}\)  (or) \(\cos C=\frac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}{2ab}\)

(ii) If two sides b and c and the included angle A are given, then

  \(\tan \left( \frac{B-C}{2} \right)=\frac{b-c}{b+c}\cot \left( \frac{A}{2} \right)\) gives \(\left( \frac{B-C}{2} \right)\)

Also, \(\frac{B+C}{2}={{90}^{o}}-\frac{A}{2}\) , so that B and C can be evaluated.

The third side is given by  \(a=b\frac{\sin A}{\sin B}\)  (or) \({{a}^{2}}={{b}^{2}}+{{c}^{2}}-2bc\cos A\)

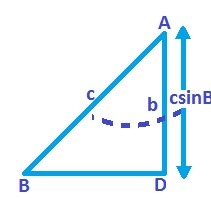
(iii) If two sides b and c and the angle B (opposite to side b) are given, then \(\sin C=\frac{c}{b}\sin B,A={{180}^{0}}-\left( B+C \right)\) , and  give the remaining elements.

Case I: b < c sinB

We draw the side c and angle B. Now, it is obvious from Fig that there is no triangle possible.