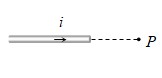
Magnetic Field Due to a Straight Wire
The Biot – Savart law allows us to calculate magnetic field due to steady current through a small element of wire. Since direction of magnetic field due to different current elements of an extended wire carrying current is not unique.
Magnetic field due to a current carrying wire at point P which lies at perpendicular distance r from the wire as shown is given as: \(B=\frac{{{\mu }_{0}}}{4\pi }\frac{i}{r}\left( \sin {{\phi }_{1}}+\sin {{\phi }_{2}} \right)\)
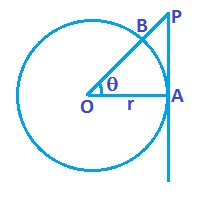
From figure, \(\alpha =\left( {{90}^{0}}-{{\phi }_{1}} \right)\) and \(\beta =\left( {{90}^{0}}+{{\phi }_{2}} \right)\) ; Hence, \(B=\frac{{{\mu }_{0}}}{4\pi }\frac{i}{r}\left( \cos \alpha -\cos \beta \right)\)
1) For a wire of finite length: Magnetic field at a point which lies on perpendicular bisector of finite length wire. \({{\phi }_{1}}={{\phi }_{2}}=\phi \) .
So, \(B=\frac{{{\mu }_{0}}}{4\pi }\frac{i}{r}\left( 2\sin \phi \right)\)
2) For a wire of infinite length: When the linear conductor XY is of infinite length and the point P lies near the center of the conductor, \({{\phi }_{1}}={{\phi }_{2}}={{90}^{0}}\)
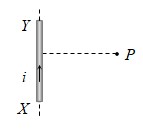
So, \(B=\frac{{{\mu }_{0}}i}{4\pi r}\left( \sin {{90}^{0}}+\sin {{90}^{0}} \right)=\frac{{{\mu }_{0}}2i}{4\pi r}\)
3) For a wire of semi – infinite length: When the linear conductor s of infinite length and the point P lies near the end Y or X. \({{\phi }_{1}}={{90}^{0}}\) and \({{\phi }_{2}}={{0}^{0}}\) .
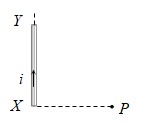
So, \(B=\frac{{{\mu }_{0}}i}{4\pi r}\left( \sin {{90}^{0}}+\sin {{0}^{0}} \right)=\frac{{{\mu }_{0}}i}{4\pi r}\)
4) For axial position of wire: When point P lies on axial position of current carrying conductor then magnetic field at P, B = 0.