Resultant Amplitude and Intensity
Intensity if the power transferred per unit area that is perpendicular to the direction of propagation of the energy. Intensity is directly proportional to square root of the amplitude. So, if intensity becomes double, then amplitude will become four times. Let us consider two waves that have the same frequency but have a certain fixed phase difference between them. Their super position shown below
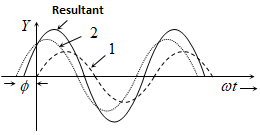
Let the two waves are:
y₁ = a₁ sin ωt and y₂ = a₂ sin (ωt + φ)
Where,
a₁, a₂ = Individual amplitudes
φ = Phase difference between the waves at an instant when they are meeting a point.
(i) Resultant Amplitude: The resultant wave can be written as: y = A sin (ωt + φ).
Where, A = Resultant Amplitude = √(a₁² + a₂² + 2a₁a₂ cosφ)
(ii) Resultant Intensity: As we know Intensity α (Amplitude) 2
I₁ = ka₁²; I₂ = ka₂² and I = kA² (k is a proportionality constant)
Resultant Intensity (I) = I₁ + I₂ + 2√I₁I₂ cosφ
For two identical sources, I₁ = I₂ = I₀ ⇒ I = I₀ + I₀ + 2√I₀I₀ cosφ = 4 I₀ cos² (φ/2).
