Regular Tetrahedron

Regular Tetrahedron

A regular tetrahedron is one in which all four faces are equilateral triangles.

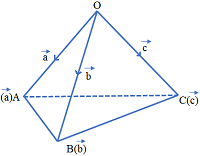
Angle between any Edge and Face not Containing that Edge of Regular Tetrahedron:

Let us find the angle between edge OA and face OBC.

Since tetrahedron is regular and its face is an equilateral triangle, the required angle is the angle between vector \(\vec{a}\)
and vector along angle bisector of \(\angle BOC\).

Let \(\vec{a},\vec{b},\vec{c}\) be the vectors.

Angle bisector of \(\angle BOC\) on \(\Delta OBC\) is along vector \(\vec{b}+\vec{c}\).

Therefore, required angle θ is the angle between vectors I.e., \(\vec{a}\) and \(\vec{b}+\vec{c}\),

\(\cos \theta =\frac{\vec{a}.\left(
\vec{b}+\vec{c} \right)}{\left| {\vec{a}} \right|\left| \vec{b}+\vec{c}
\right|}\),

\(=\frac{\vec{a}.\vec{b}+\vec{a}.\vec{c}}{\left|
\vec{b}+\vec{c} \right|}\),

\({{\left| \vec{b}+\vec{c}
\right|}^{2}}={{b}^{2}}+{{c}^{2}}+2\vec{b}.\vec{c}\times \cos \theta \),

\(=1+1+2(1)(1)\cos {{60}^{o}}\),

= 1+ 1 + 2 (½)

= 1 + 1 + 1 = 3

\(\left| \vec{b}+\vec{c}\right|=\sqrt{3}\),

\(\cos \theta
=\frac{\vec{a}.\vec{b}+\vec{a}.\vec{c}}{\left| \vec{b}+\vec{c} \right|}\),

\(\cos \theta =\frac{1.1.\cos
{{60}^{o}}+1.1.\cos {{60}^{o}}}{1\times \sqrt{3}}\),

\(\cos \theta =\frac{1/2+1/2}{\sqrt{3}}\),

\(\cos \theta =\frac{\frac{2}{2}}{\sqrt{3}}\),

\(=\frac{1}{\sqrt{3}}\).

\(\theta ={{\cos }^{-1}}\left( \frac{1}{\sqrt{3}} \right)\).