Direction Cosines: the cosines of the angles made by a directed line segment with the coordinate axes are called as the direction cosines of that line.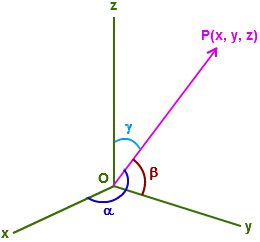
if α, β, and γ are the angles made by the line segment with the coordinate axis then these angles are termed to be the direction angles and the cosines of these angles are the direction cosines of the line. Hence, cos α, cos β and cos γ are called as the direction cosines and are usually denoted by l, m and n.
l = cos α, m = cos β and n = cos γ
Direction Ratios: Three numbers which are proportional to the direction cosines of a line are called as the direction ratios. Hence, if ‘a’, ‘b’ and ‘c’ are the dr’s and l, m, n are the dc’s then, we must have \(\frac{a}{l}=\frac{b}{m}=\frac{c}{n}\)
Relation between the Direction Cosines: Let OP be any line through the origin O which has direction cosines l, m, n.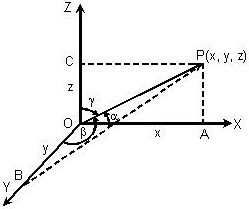
Let P be the point having coordinates (x, y, z) and OP = r
Then OP2 = x² + y² + z² = r² …. (1)
From P draw PA, PB, PC perpendicular on the coordinate axes, so that OA = x, OB = y, OC = z.
Also, ∠POA = α, ∠POB = β and ∠POC = γ.
From triangle AOP, l = cos α = x/r ⇒ x = lr
Similarly y = mr and z = nr
From equation 1
r² (l² + m² + n²) = x² + y² + z² = r²
⇒ l² + m² + n² = 1
Problems: If a line makes angles \(\frac{\pi }{3}\) and \(\frac{\pi }{4}\) with the x – axis and y – axis respectively, then the angle made by the line with z-axis is
Solution: cos²α + cos²β + cos²γ = 1
Given that \(\alpha \,=\,\frac{\pi }{3}\),\(\beta =\,\frac{\pi }{4}\)
cos²γ = ¼
cosγ = ½
\( \gamma \,=\,\frac{ \pi }{3}\)