According to the first law of motion given by Newton says that a body is in its current motion state till any external force is acted upon it. The moment of inertia of the linear motion is measured by the mass of the system and angular counterpart. The inertia is related to mass and the amount of mass distribution throughout the body. It is not necessary to be possessing same moment of inertia by two bodies of the same mass. Thus, the inertia shows that how tough a body to move.
If an object possess more inertia then it is very to move it or stop it; for example, the inertia of heavy truck is more than a person. It also shows how hard is spinning of an object with respect to certain axis which depends on mass and location of mass. This spinning difficulty around an axis is the moment of inertia. Let’s discuss more on that.
What is Moment of Inertia?
The concept of moment of inertia was introduced by Leonhard Euler. The resistance that is shown by the object to change its rotation is called moment of inertia. I and J are used as symbols for denoting moment of inertia. The moment of inertia describes the angular acceleration produced by an applied torque. It depends on the shape and mass distribution of the body, and on the orientation of the rotational axis.
The moment of inertia plays the same role for rotation as the mass does for a translational motion, it describes the resistance of a body to a change of its state of motion. The difficulty faced to change the angular motion of any object about an axis is shown or given or measured by calculating moment of inertia about that particular axis.
Inertia in rotational motion is analogous to mass in linear motion. To explain it in a better let’s consider the example of a rotating disc. The kinetic energy of the disc can be represented as,
K.E = ½ ∑mᵢvᵢ²
But as we know in this case each mass does not have same linear velocity hence it is easier to realize using angular velocity which is equal for all the masses. We also know, v = ωr.
Substituting the value we get,
K.E = ½ ∑mᵢrᵢ²ω²
K.E = ½ (∑mᵢrᵢ²)ω²
From the above equation we get, ∑mᵢrᵢ² is the moment of inertia of the system. Unit of moment of inertia is kg.m².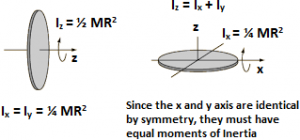
There are two theorems which are used to calculate moment of inertia about any arbitrary axis. They are parallel axis and perpendicular axis theorem. According to parallel axis if the moment of inertia of a body about a particular axis is I. Then the moment of inertia of the body about an axis having perpendicular distance of d from the given axis is:
Id = I + Md²
Now according to perpendicular axis theorem, if the moment of inertia is I about z – axis. If we select two perpendicular axis such that these two are mutually perpendicular to the original axis i.e. x – axis and y – axis then we can state that,
Iz = Ix + Iy
Generally we choose axis such that Ix = Iy, so that calculations become easy. Also we can represent all moment of inertia as follows,
I = MK²
Here, K is known as radius of gyration about the considered axis. Values of moment of inertia for some of the common bodies are:
Solid cylinder about central axis = ½ MR²
Solid sphere about a diameter = ⅖ MR²
Moment of inertia of ring perpendicular axis = MR²
Moment of inertia of disc about perpendicular axis = ½ MR².
Steps to Calculate Moment of Inertia?
Calculating the moment of inertia involves a few steps:
- Find out the point or the axis of rotation of the object of the body, find the coordinates of the point.
- If the moment of inertia has to be calculated over x axis then integrate.
- Similarly the moment of inertia is found for y axis as well.
- It is simple integral we need to solve and it can be computed using the formula described above.
How to find the Moment of Inertia?
Problem: Find the moment of inertia of the ball having mass of 10kg and radius of 5cm?
Solution: Given,
Mass of the ball = 10 kg
Radius = 5 cm = 0.05 m
Moment of Inertia of the ball =?
We know that:
Moment of Inertia (I) = MR²
= 10 × (0.05)²
= 0.025 kg.m².
Therefore, the Moment of Inertia is 0.025 kg.m².