Motion of two bodies one resting on the other – 2nd Condition
When a body A of mass m is resting on a body B of mass M then two conditions are possible:
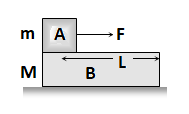
2) A force F is applied to the lower body and then following four situations are possible
i) When there is no friction:
a) B will move with acceleration while A will remain at rest as there is no pulling force on A.
\({{a}_{B}}=\left( \frac{F}{M} \right)\) and aA = 0.
b) As relative to B. A will move backwards with acceleration and so will fall from it in time t.
∴ \(t=\sqrt{\frac{2L}{a}}=\sqrt{\frac{2ML}{F}}\).
ii) If friction is present between A and B only and F < F’l:
Where, F’ = Pseudo force on body A and Fl = Limiting friction between body A and B.
a) Both the body will move together with common acceleration, \(a=\frac{F}{M+m}\).
b) Pseudo force on the body A, \({{F}^{‘}}=mq=\frac{mF}{m+M}\) and Fl = μsmg.
c) \({{F}^{‘}}<{{F}_{l}}\Rightarrow \frac{mF}{m+M}<{{\mu }_{s}}mg\) ⇒ F < μs (m + M) g, so both bodies will move together with acceleration \({{a}_{A}}={{a}_{B}}=\frac{F}{m+M}\), if F < μs (m + M) g
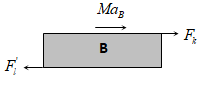
iii) If friction is present between A and B only and F > F’l:
Where, F’l = μsmg = Limiting friction between body A and B, both the body will move with different acceleration. Here force of kinetic friction μkmg will oppose the motion of B while will cause the motion of A.
Acceleration of body A relative to B will be: \(a={{a}_{A}}-{{a}_{B}}=-\left[ \frac{F-{{\mu }_{k}}g\left( m+M \right)}{M} \right]\), here -ve sign implies that relative to B, A will move backwards and will fall it after time.
\(t=\sqrt{\frac{2L}{a}}=\sqrt{\frac{2ML}{F-{{\mu }_{k}}g\left( m+M \right)}}\).
iv) If there is friction between B and floor and F > F’l :
Where, F’l = μs (m + M) g = Limiting friction between body B and surface
The system will move only if F > F’lthen replacing F by F – F’l. The entire case (iii) will be valid. However, if F > F’lthe system will not move andfriction between B and floor will be F while between A and B is zero.
