MAXIMA AND MINIMA PROBLEMS
1. Without using the derivative, show that f(x) = (½)x is strictly decreasing on R.
Solution: Given that f(x) = (½)x
Let x₁, x₂ ϵ R
Let x₁ < x₂ ⇒ (½)x₁ > (½)x₂
⇒ f(x₁) > f(x₂).
∴ f is strictly decreasing on R.
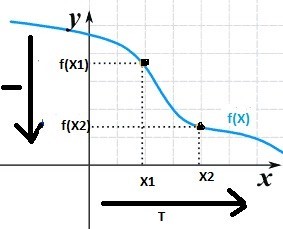
2. Without using the derivative, show that f(x) = 3x + 7 is strictly decreasing on R
Solution: f(x) = 3x + 7
Let x₁, x₂ ϵ R
Let x₁ < x₂ 3x₁ < 3x₂
⇒ 3x₁ + 7 < 3x₂ + 7
⇒ f(x₁) < f(x₂)
⇒ f is strictly decreasing on R
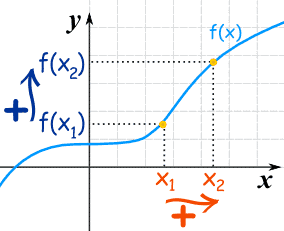
3. Show that x+1/x is increasing on [1, ∞)
Solution: f(x) = x + 1/x
f‘ (x) = 1 – 1/x²
Since x ϵ [1, ∞), 1 – 1/x² > 0
⇒ f’(x) > 0
Therefore f(x) is increasing function
4. State the point at which the following functions are increasing and the points at which they are decreasing f(x) = x³ – 3x²
Solution: f(x) – x³ – 3x²
f’(x) = 3x² – 6x = 3x (x-2)
f(x) is increasing function f’(x) > 0
3x (x – 2) > 0
Therefore x does not lie between 0 and 2
Therefore f(x) is increasing in (-∞, 0) È (2, ∞)
f(x) is decreasing if f’(x) < 0
x (x – 2) < 0
x lies between 0 and 2
f(x) is decreasing in (0, 2)
