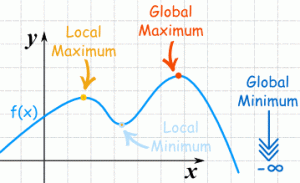
Global Maxima or Minima
Global Maxima or Minima in [a, b]: Global maxima or minima of f(x) in [a, b] is basically the greatest or least value of f(x) in [a, b]. Mathematically, it is written as:
The function f(x) has a global maximum at the point ‘a’ in the interval I if f (a) ≥ f(x), for all x ∈ I.
Similarly, f(x) has a global minimum at the point ‘a’ if f (a) ≤ f (x), for all x ∈ I.
Global maxima or minima in [a, b] will always occur either at the critical points of f(x) within [a, b] or at the end points of the interval.
Steps to find out the global maxima or minima in [a, b]
Step 1: Find out all the critical points of f(x) in (a, b). Let C₁, C₂, … Cn be the different critical points.
Step 2: Find the value of the function at these critical points and also at the end points of the domain. Let the values of the function at critical points be f(C₁), f(C₂) … f(Cn).
Step 3: Find M₁ = max{f(a), f(C₁), f(C₂) … f(Cn), f(b)} and M₂ = min{f(a), f(C₁), f(C₂) … f(Cn), f(b)}. Now M₁ is the maximum value of f(x) in [a, b] and M₂ is the minimum value of f(x) in [a, b].
Problem: find two positive numbers whose sum is 12 and the sum of the squares is minimum
Solution: Let x and y be given number
x + y = 12
Y = 12 – x
Let f (x) = x² + y²
f (x) = x² + (12 – x)²
= x² + 144 + x² – 24x
= 2x² – 24x + 144
f’(x) = 4x-24 and f‘‘(x) = 4
For maxima and minima, f‘(x) = 0 4x – 24 = 0
4x – 24 = 0 x = 24/4 = 6
f’’(x) = 4 > 0
f (x) has minimum when x = 6
y = 12 – x = 12 – 6 = 6
The numbers are 6, 6.
