Locus of Point of Intersection of Tangent under Different Conditions
Tangent to the parabola y² = 4ax at point P (at₁², 2at₁) and Q (at₂², 2at₂) are t₁ y = x +at₁² and t₂ y = x + at₂² respectively. These tangents intersect at point R (at₁t₂,a (t₁ + t₂).
If we want to find the locus of point R under some condition, then let point R hascoordinates (h, k).
We have h = at₁t₂ and k = a (t₁ + t₂).
Example: Find the locus of the point of intersection of tangent to the parabola y² = 4ax
(i) which are include at an angle θ to each other.
(ii) which intercept constant length c on the tangent at the vertex.
Solution:
(i) Given that
\(\tan \theta =\left| \frac{\frac{1}{{{t}_{2}}}-\frac{1}{{{t}_{1}}}}{1+\frac{1}{{{t}_{1}}}\frac{1}{{{t}_{2}}}} \right|=\left| \frac{{{t}_{1}}-{{t}_{2}}}{1+{{t}_{1}}{{t}_{2}}} \right|\).
tanθ (1 + t₁t₂²) = (t₁ – t₂)²
tanθ (1 + t₁t₂²) = (t₁ + t₂)² + 4t₁t₂
We have h = at₁t₂ and k = a (t₁ + t₂)
\({{\tan }^{2}}\theta {{(1+\frac{h}{a})}^{2}}={{(\frac{k}{a})}^{2}}+4\times \frac{h}{a}\).
tan²θ (x + a)²= (y)² + 4a
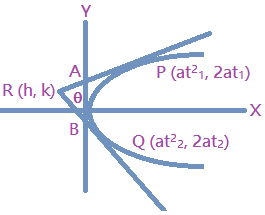
(ii) point A and B have coordinate (0, at₁) and (0, at₂) respectively
Given AB = c
|at₁ – at₂| = c
a² [(t₁ + t₂)² – 4t₁t₂] = c²
We have h = at₁t₂ and k = a (t₁ + t₂)
\({{a}^{2}}\left[ {{\left( \frac{k}{a} \right)}^{2}}-4\times \frac{h}{a} \right]={{c}^{2}}\).
y² – 4ax = c²
Which is parabola.
