Capacity of Parallel – Plate Capacitor with Dielectric
When a dielectric material is placed between the plates of a capacitor, the capacitance of the capacitor increases.These are non-conductors up to a certain value of field depending upon their nature.If the field exceeds the limiting value, called dielectric strength, dielectric loses its insulating property and beings to conduct.
Suppose a parallel – plate capacitorhas a plate area A and a separation d and a dielectric slab of thickness t and area A is inserted between the plates.
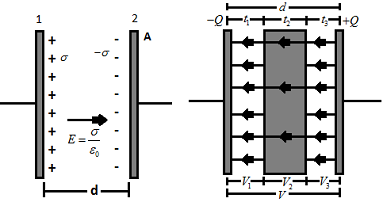
Let Q be the charge given to the capacitor plates. The electric field between the plates of the capacitor is given by \(E=\frac{\sigma }{{{\varepsilon}_{0}}}=\frac{Q}{A{{\varepsilon }_{0}}}\).
The electric field in the region of dielectric slab is \({{E}^{‘}}=\frac{E}{K}=\frac{Q}{K{{\varepsilon }_{0}}A}\).
We know that if electric field is constant, then potential difference between two points separated by distance d along the field line is Ed.
Therefore, the potential difference between two plates is:
\(V={{V}_{1}}+{{V}_{2}}+{{V}_{3}}=E{{t}_{1}}+{{E}^{‘}}{{t}_{2}}+{{E}^{‘}}{{t}_{3}}=\frac{Q}{{{\varepsilon }_{0}}A}{{t}_{1}}+\frac{Q}{K{{\varepsilon }_{0}}A}{{t}_{2}}+\frac{Q}{{{\varepsilon }_{0}}A}{{t}_{3}}\).
\(V=\frac{Q}{A{{\varepsilon }_{0}}}({{t}_{1}}+{{t}_{2}})+\frac{Q}{K{{\varepsilon }_{0}}A}{{t}_{2}}=\frac{Q}{{{\varepsilon }_{0}}A}(d-t)+\frac{Q}{K{{\varepsilon }_{0}}A}t\).
\(Capacity(C)\,\,=\,\,\frac{Q}{V}\,\,=\,\,\frac{Q}{\frac{Q}{{{\varepsilon }_{0}}A}(d-t)+\frac{Q}{K{{\varepsilon }_{0}}A}t}=\frac{1}{\frac{(d-t)}{{{\varepsilon }_{0}}A}+\frac{t}{K{{\varepsilon }_{0}}A}}\).
\(Capacity(C)\,\,=\,\,\frac{Q}{V}\,\,=\,\,\frac{{{\varepsilon }_{0}}A}{(d-t)+\frac{t}{K}}\).
