Locus – Algorithm

Definition of Locus: In geometry, a locus is a set of all points (commonly, a line, a line segment, a curve or a surface), whose location satisfies or is determined by one or more specified conditions.

Equation to the Locus of a Point: The equation to the locus of a point is the relation which is satisfied by the coordinates of every point on the locus of the point.

Algorithm to find the Locus of a Point:

i. Assume the coordinates of the point (h, k) whose locus to be found.

ii. Write the given condition in mathematical form involving h, k

iii. Eliminate the variables if any

iv. Replace h by x and k by y in the result (3).

Example: Find the equation of locus of a point which is equidistance from the coordinate’s axes.

Solution: Let P(x, y) be any point in the locus.

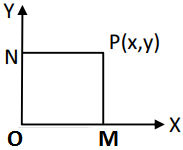
Let PM = perpendicular distance of P from X- axis. = |x|.

let PN = perpendicular distance of P from Y – axis = |y|.

Given condition PM = PN

|x| = |y|

Squaring on both sides

x² = y²

∴ Locus of P is x² – y² = 0.