1st Law / Junction Rule:
Across any junction algebraic sum of all currents is zero; this is a consequence of Conservation of charge principle.
2nd Law / Loop Rule:
This is a consequence of conservation of energy principle. Across any loop i.e. closed path work done by all agents is equal to zero. This follows from the fact that in a circuit the drift speed of electrons remains constant.
Following convention can be used to apply Kirchhoff’s law.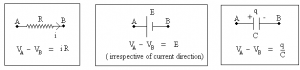
Illustration 1: A battery of e.m.f 2.0 volts and internal resistance is being charged with a current of 5.0 A. What is the potential difference between the terminals of the battery
Solution: As the battery is being charged, the current goes into the positive terminal as shown in the figure. The potential drop across the internal resistance is
5.0 x 0.10Ω = 0.50 V
Hence, the potential drop across the terminals will be 2.0 V + 0.50 V = 2.5 V
Illustration 2: Determine the current in each branch of the network shown in the figure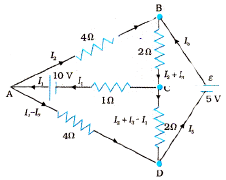
Solution: Each branch of the network is assigned an unknown current to be determined by the application of Kirchhoff’s rules. To reduce the number of unknowns at the outset, the first rule of the Kirchhoff’s is used at every junction to assign the unknown current in each branch. We then have three unknown current in each branch. We then have three unknowns I₁I₂ and I₃ which can be found by applying the second rule of Kirchhoff to three different closed loops. Kirchhoff’s second rule for the closed loop ADCA gives,
10 – 4 (I₁ – I₂) + 2 (I₂ + I₃ – I₁) – I₁ = 0
i.e, 7I₁ – 6I₂ – 2I₃ = 10
For the closed loop ABCA, we get
10 – 4I₂ – 2 (I₂ + I₃) – I₁ = 0
i.e, I₁ + 6I₂ + 2I₃ = 10
For the closed loop BCDEB,
5 – 2 (I₂ + I₃) – 2 (I₂ + I₃ – I₁) = 0.
we get I₁ + 6I₂ + 2I₃ = 10
For the closed loop BCDEB, we get
5 – 2 (I₂ + I₃) – 2 (I₂ + I₃ – I₁) = 0 i.e, 2I₁ – 4I₂ – 4I₃ = -5
Equations are three simultaneous equations in three unknowns. These can be solved by the ususal method to give I₁ = 2.5 A, I₂ = 5/8 A, I₃ = \(1\frac{7}{8}\)A
The currents in the various branches of the network are
\(AB:\frac{5}{8}A,\,CA:2\frac{1}{2}A,\,DEB:1\frac{7}{8}A\)
\(AD:1\frac{7}{8}A,\,CD:0A,\,BC:2\frac{1}{2}A\)
It is easily verfied that Kirchhoff’s second rule applied to the remaining closed loops does not provide any additonal independent equation, that is, the above values of currents satisfy the second rule for every closed loop of the network. For example, the total voltage drop over the closed loop BADEB.
\(5V+\left( \frac{5}{8}\times 4 \right)V-\left( \frac{15}{8}\times 4 \right)V\) is equal to zero, as required by Kirchhoff’s second rule.