The motion of an object has the energy that constitutes the Kinetic energy. The energy of any system is the capacity of doing any work. This is mainly classified into kinetic energy and potential energy. But it is always found according to its nature like when it is in form of heat then it’s a thermal energy, work can be done in mechanical ways etc. Thus, according to work and system, it is transform from one form to another form of energy and remains constant for system to follow the conservation law of energy. Different forms of energy are related to motion of particles.
If a body is in static state then it contains potential energy but when it is thrown then its potential energy is converted into kinetic energy.
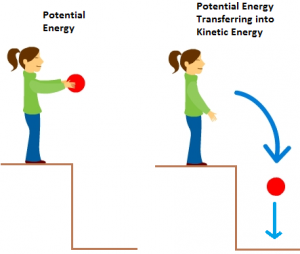
Similar to spring or in bow contains potential energy in the rest condition due to their configuration. Nuclear energy is also potential energy due to the configuration of fundamental subatomic particles that present in the nucleus of an atom.
Formula to Calculate Kinetic Energy: To simply put, Kinetic energy can be calculated by the basic process of computing the work (W) that is done by a force (F). If the body has a mass of m that was pushed for a distance of d on a surface with a force that’s parallel to it.
W = F x d = m x a x d
The acceleration in this equation can be substituted by the initial (vi) and final (vf) velocity and the distance. This we get from the kinematic equations of motion.
W = m x a x d
\(W\,=\,m\,\times \,d\,\times \,\frac{{{v}_{f}}^{2}\,-\,{{v}_{i}}^{2}}{2d}\).
\(W\,=\,m\,\times \,\frac{{{v}_{f}}^{2}\,-\,{{v}_{i}}^{2}}{2d}\).
\(W\,=\,\frac{1}{2}\times m\times {{v}_{f}}^{2}\,-\,\frac{1}{2}\times m\times {{v}_{i}}^{2}\).
The Kinetic Energy (K.E) basic quantity ½ mv² changes when a particular sum of work is acted upon an object.
K.E = ½ mv²
The total work that is done on a system is equivalent to the change in kinetic energy. Thus,
Wnet = Δ K.E
This equation is known as the work-energy theorem and has large applications even if the forces applied varies in magnitude and direction. This factor is an important one in the concept of conservation of energy.
Kinetic Energy Units: Dimensionally, the kinetic energy of any object is equivalent to the product of its mass and the square of its velocity. In fps system of units, the unit of kinetic energy is lbm – (ft/sec)². In system of units, the unit of kinetic energy becomes as kgm²/sec²better knows an Joule.
Examples of Kinetic Energy:
- A semi-truck travelling down the road has more kinetic energy than a car travelling at the same speed because the truck’s mass is much more than the Car’s.
- A river flowing at a certain speed comprises kinetic energy as water has certain velocity and mass.
How to Calculate Kinetic Energy?
Example: If we throw a body upwards with velocity of 4ms¯¹, then at what height its kinetic energy reduces to half of the initial value? Take g = 10 ms¯²
Initial Energy = ½ x m x (4)² = (8m)m/sec²
Let kinetic energy at a height h be 8/2 = 4 m/sec²
It will also be equal to the potential energy.
Hence, K.E = P.E
½ mv² = mgh
(4m) = m x 10 x h
h = 0.4m.
