Hyperbola – Tangent and Normal

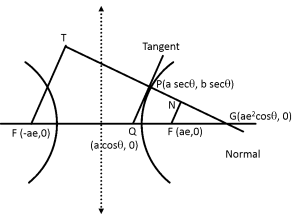
Tangent to the Hyperbola: Let S = 0 be a hyperbola and P be a point on the hyperbola

Let Q be any other point on the hyperbola. If the secant line PQ approaches to the same limiting position as Q moves along the curve and approaches to P from either side, then the limiting position is called a tangent line or tangent to the hyperbola at P. the point P is called of contact of the tangent to the hyperbola.

If L = 0 is a tangent to the hyperbola S = 0 at P, then we say that the line L = 0 touches the hyperbola S = 0 at P.
The equation of the tangent to the hyperbola S = 0 at P (x₁, y₁) is S₁ = 0.

Example: Find the equation of the tangent to the hyperbola 3x² + 4y² = 8 at P (2, -1)

Solution: Given that

3x² + 4y² = 8 at P (2, -1)

We can use formula is S₁ = 0

The equation of a tangent is 3xx₁ + 4yy₁ = 8

x₁ = 2, y₁ = -1

3x (2) + 4y (-1) = 8

6x – 4y = 8

3x – 2y – 4 = 0

Normal to the Hyperbola: Let S = 0 be a hyperbola and P be a point on the hyperbola S = 0. The line passing through P and perpendicular to the tangent of S = 0 at P is called the normal to the hyperbola S = 0 at P.

The equation of the normal to the hyperbola \(\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{{{y}^{2}}}{{{b}^{2}}}=1\) at P (x₁, y₁) is \(\frac{{{a}^{2}}x}{{{x}_{1}}}+\frac{{{b}^{2}}y}{{{y}_{1}}}={{a}^{2}}+{{b}^{2}}\).

Example: Find the equation of the normal to the hyperbola 3x² – 2y² = 30 at P (4, -3)

Solution: Given 3x² – 2y² = 30 at P (4, -3)

Equation of the hyperbola is 3x² – 2y² = 30 at P (4, -3)

x²/10 – y²/15 = 1

Equation of the normal is 10x/4+ 15y/-3 = 10 +15

10x/4+ 15y/-3 = 25

5x/2 – 5y = 25

5x – 10y = 50

x – 2y = 10

x – 2y – 10 = 0.