Drift Velocity
In absence of Electric field, electrons in a conductor will be moving due to thermal motion during which they collide with the fixed ions. An electron colliding with an Ion emerges with the same speed as before the collision. However, the direction of its velocity after the collision is completely random.
What is Drift Velocity?
The average velocity attained by some particle such as an electron due to the influence of an electric field is termed as the drift velocity. The movement or the motion of the particles is assumed to be along a plane and hence the motion can also be referred to as the axial drift velocity.
Subatomic particles like electrons move in random directions all the time, when electrons are subjected to an electric field they do move randomly but they slowly drift in one direction, in the direction of the electric field applied, the net velocity at which these electrons drift is known as drift velocity.
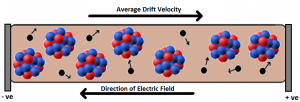
Formula to find the Drift Velocity?
Drift velocity of electron in a conductor of constant cross-sectional area is \({{V}_{d}}\,\,=\,\,\frac{I}{n\,A\,q}\).
Where,
V = Drift Velocity of the Electrons.
I = Current flowing through the Conductor.
A = Cross – Sectional Area of the Conductor.
q = Charge on the Charge Carrier.
How to find the Drift Velocity?
Problem: A current of 4A that is flowing in a copper conductor with a cross section of 1mm², find the drift velocity?
Solution: Given,
Current (I) = 4A
Cross – Sectional Area (A) = 1mm² = 10⁻⁶ m²
We know that for Copper, n = 8.5 x 10²⁸/ m³
Charge of an Electron, q = 1.6 x 10⁻¹⁹ C
Now, we know that:
\(Drift\,\,Velocity({{V}_{d}})\,\,=\,\,\frac{I}{n\,A\,q}\).
\({{V}_{d}}\,=\,\frac{4}{8.5\times {{10}^{28}}\times 1\times {{10}^{-6}}\times 1.6\times {{10}^{-19}}}\,=\,\frac{4}{13.6\times {{10}^{3}}}\,=\,2.94\times {{10}^{-4}}m/\sec \).
Therefore,
Drift Velocity (Vd) = 2.9 x 10⁻⁴ m/sec
