Friction

Generally accey body surface is rigid (micro seopic view)

If we go for a microscopic view the surfaces like.

So due to this rigidness the inter locking will occur between the two bodies. When there in contact tis inter locking should be in order to move the body on the other (or surface) this opposition force created due to interlocking is called friction.

Types of friction:

Static friction

Kinetic friction

Static friction (f_s): The friction force offered for the body which is at rest is called Static friction.

Kinetic friction (f_k): The friction force offered for the body which is in motion is called Kinetic friction.

Generally we know that friction is due to the inter locking of two surfaces these interlocking will be more when the body is at rest and less when the body is in motion.

So obviously we can say that static friction will be more than the Kinetic friction.

Generally any friction force it may be either static or kinetic completely depends upon the normal reaction.

f_s α N

f_s = μ_s N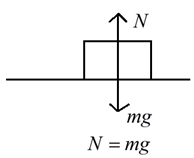μ_s = Coefficient of static friction

f_k α N

f_k = μ_k N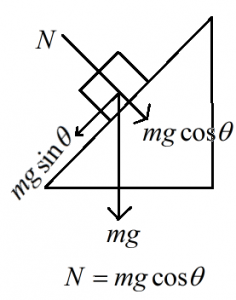μ_k = Coefficient of kinetic friction

We know

f_s > f_k

μ_s N > μ_k N

=> μ_s > μ_k

→ Lans of friction → limits repose

Definition:- 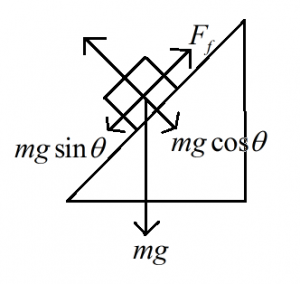The body just starts sliding

mgsinθ = F_f

mgsinθ = μ_s mg cos θ

= tan θ = μ_s

θ = tan^-1 (μ_s)

Angle of friction:-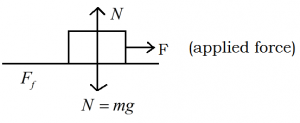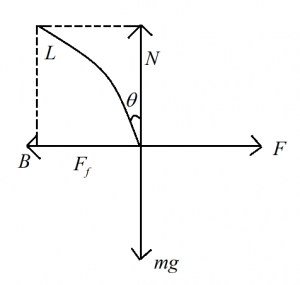N = normal reaction

Let the horizontal force applied (F) makes the block just to slides, i.e., the frictional force is equal to the limiting friction.

When this condition is satisfied, the angle which the resultant makes the vertical [or angle between the normal and external force] is called the angle of friction.

tan θ = limiting friction / Normal reaction … (1)

But we also know that

Limiting friction = μ_s x Normal reaction

=> limiting friction / Normal reaction = μ_s … (2)

From equation (1) & (2) [(1) = (2)]

We get

tan θ = μ_s

θ = tan^-1 (μ_s)

=> θ = Angle of friction.

Example: The two blocks, m = 16 kg and M = 88 kg shown in the figure are free to move. The coefficient of static friction between the blocks is µs = 0.38, but the surface beneath M is frictionless. What is the minimum horizontal force F required to hold m against M?Solution: Draw the free body diagram of both the blocks.

Fix = max, Fiy = may, F – N = ma … (1)

fs = mg

µ N = fs = mg … (2)

= f/N

Since    f = µN, therefore tan = µ

For block M, N = Ma … (3)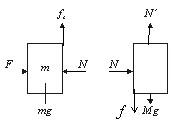From equation (1), (2) and (3), we get

\(F-\frac{mg}{\mu }=\frac{m}{M}\,.\,\frac{mg}{\mu }\)

F = mg \(\left[ \frac{m+M}{\mu M} \right]\) = 16 × 9.8\(\left[ \frac{104}{0.38\times 88} \right]\)  = 487.65 N