GREATEST INTEGER FUNCTION: For any real numbers x, we denote [x], the greatest integer less than or equal to x.
For example, [2.45] = 2, [-2.1] = -3, [1.75] = 1, [0.32] = 0 etc.
The function f defined by f (x) = [x] for all x ϵ R, is called the greatest integer function.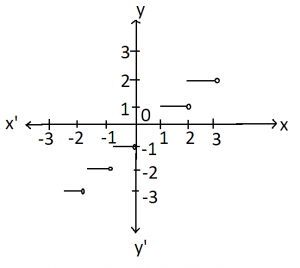
In general, if n is an integer and x is any number satisfying n ≤ x < n+1, then [x] = n.
Also, if [x] denotes the fractional part of x, then [x] = x- [x] or x = [x] + [x].
PROPERTIES OF GREATEST INTEGER FUNCTION: If n is an integer and x is any real number between n and n+1, then the greatest integer function has the following properties:
i) [-n] = – [n]
ii) [x+n] = [x] + n
iii) [-x] = -[x] – 1
iv) \(\left[ x \right]+\left[ -x \right]=\left\{ \begin{align}& -1,\,\,\,\,if\,\,\,x\notin Z \\& 0,\,\,\,\,if\,\,x\in Z \\\end{align} \right.\)
v) \(\left[ x \right]-\left[ -x \right]=\left\{ \begin{align}& 2\left[ x \right],\,\,\,\,if\,\,\,x\in Z \\& 2\left[x\right]+1,\,\,\,\,if\,\,x\notin Z \\\end{align} \right.\)
vi) [x] ≥ n => [x] ≥ n, where n ϵ Z
vii) [x] ≤ n => x < n+1, n ϵ Z
viii) [x] > n => x ≥ n+1, n ϵ Z
ix) [x] < n => x < n, n ϵ Z
x) [x+y] = [x] + [y + x – [x]] for all x, y ϵ R.
xi) \(\left[ x \right]+\left[ x+\frac{1}{n}\right]+\left[ x+\frac{2}{n} \right]+…..+\left[ x+\frac{n-1}{n} \right]=\left[ nx\right],\,\,n\in N\)
SIGNUM FUNCTION: The function defined by
\(f\left( x \right)=\left\{ \begin{align}& \frac{\left| x \right|}{x},\,\,x\ne 0 \\& 0\,\,\,\,,\,\,x=0 \\\end{align} \right.\)
Or, \(f\left( x \right)=\left\{ \begin{align}& 1,\,\,x>0 \\& 0,\,\,x=0 \\& -1,\,\,x<0 \\\end{align} \right.\)
Is called the signum function.
The domain of the signum function is R and the range is the set {-1, 0, 1}. The graph of this function is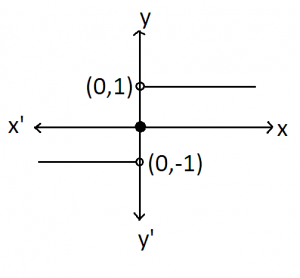
PERIODIC FUNCTIONS:
Periodic Functions: A function f (x) is said to be a periodic function if there exists a positive real number T such that f (x + T) = f (x) for all x ϵ R.
We know that
sin (x + 2π) = sin (x + 4π) = … = sin x
And,
cos (x + 2π) = cos (x + 4π) = … = cos x for all x ϵ R.
Therefore, and are periodic functions.
PEROID: If f (x) is a periodic function, then the smallest positive real number T is called the period or fundamental period of function f (x) if f (x + T) = f (x) for all x ϵ R..
In order to check the periodicity of a function f (x), we follow the following algorithm.
SOME USEFUL RESULTS ON PERIODIC FUNCTIONS:
RESULT 1: If f (x) is a periodic function with periodic T and a, b ϵ R such that a ≠ 0, then a f (x) + b is periodic with period T.
RESULT 2: If f (x) is a periodic function with period T and a, b ϵ R such that a ≠ 0, then f (ax + b) is periodic with period T / |a|.
RESULT 3: Let f (x) and g (x) be two periodic functions such that:
Period of f(x) = m/n, where m, n ϵ N and m, n are co-prime.
And,
Period of g(x) = r/s, where r ϵ N and s ϵ N are co-prime.
Then, (f + g) (x) is periodic with period T given by T = LCM of (m, r) / HCF of (n, s)
Provided that there does not exist a positive number k < T for which f (k + x) = g(x) and g (k + x) = f(x) else k will be the period of (f + g) (x).
The above result is also true for functions f/g, f – g and fg.
Example: Find the period of f (x) = 5sin3x – 7sin8x
Solution: We observe that:
Period of 5sin 3x is 2π / 3
Period of 7 sin 8x is 2π / 8 = π/ 4
∴ Period of f (x) = LCM of 2π and π / HCF of 3 and 4= 2π / 1 = 2π