Equation of a Plane Passing through Two Parallel Lines
Let the plane pass through parallel lines \(\vec{r}=\vec{a}+\lambda \vec{b}\) and \(\vec{r}=\vec{c}+\mu \vec{b}\).
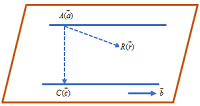
As shown in the diagram, for any position of R in the plane, vectors \(\overrightarrow{RA}\), \(\overrightarrow{AC}\) and \(\vec{b}\) are coplanar. Then \(\left[ \vec{r}-\vec{a}\vec{c}-\vec{a}\vec{b} \right]=0\), which is the required equation of the plane.
Equation of Plane Parallel to a Given Plane:
The general equation of the plane parallel to the plane ax + by + cz + d = 0 is ax + by + cz + k = 0, where k is any scalar, as normal to the both planes is \(a\hat{i}+b\hat{j}+c\hat{k}\).
Example: Find the equation of the plane passing through (3, 4, -1), which is parallel to the plane \(\vec{r}.\left( 2\hat{i}-3\hat{j}+5\hat{k} \right)+7=0\).
Solution: The equation of any plane which is parallel to \(\vec{r}.\left( 2\hat{i}-3\hat{j}+5\hat{k} \right)+7=0\) is
\(\vec{r}.\left( 2\hat{i}-3\hat{j}+5\hat{k} \right)+\lambda =0\) … (i)
2x – 3y + 5z + λ = 0
(3, 4, -1) is passing through equation (i)
2 (3) – 3 (4) + 5 (-1) + λ = 0
6 – 12 – 5 + λ = 0
λ = 11
Required equation is \(\vec{r}.\left( 2\hat{i}-3\hat{j}+5\hat{k} \right)+11=0\).
