Acceleration of Block against Friction
Newton’s second law says that the acceleration (a) of an object is proportional to the force (F) applied on it, and the proportionality factor is the object’s mass (m). Force is a vector quantity, which means we must consider the direction in which it acts. Two main types of frictional forces exist: The static force and the sliding force.
a) Acceleration of a block on Horizontal Surface: When body is moving under application of force P, then kinetic friction opposes its motion.
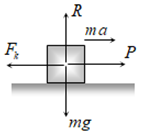
Let, a is the net acceleration of the body, from the figure ma = P – Fk ⇒ \(a\,=\frac{P-{{F}_{k}}}{m}\).
b) Acceleration of a block sliding down over a rough Inclined Plane: When angle of inclined plane is more than angle of repose, the body placed on the inclined plane slides down with acceleration (a).
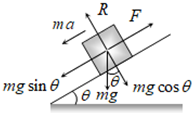
From the figure: ma = mg sin θ – F ⇒ ma = mg sin θ – μR
⇒ ma = mg sin θ – μmg sin θ
Therefore, Acceleration (a) = g (sin θ – μ cos θ)
c) Retardation of a block sliding up over a rough Inclined Plane: When angle of inclined plane is less than angle of repose, then for the upward motion,
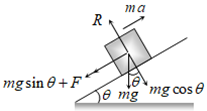
⇒ ma = mg sin θ + F ⇒ ma = mg sin θ + μ mg cos θ
Retardation, (a) = g (sin θ + μ cos θ)
